Minds On
Patterns

Some key ideas about patterns:
- Patterns can be extended because something in them repeats.
- Pattern rules describe how a pattern repeats, grows or shrinks. They can be described in words, or with letters and numbers. Pattern rules help us extend patterns, make predictions, and figure out missing numbers.
- Patterns can be extended in multiple directions, showing what comes next or what came before.
Let’s explore a hundred chart together! If possible, your teacher will show you how to use the hundred chart and then you can try using it yourself.
A hundred chart is filled with patterns. Explore the hundred chart by recording the numbers you land on when you skip count by 3, starting at 36, for 6 terms.
Next, explore the hundred chart by recording the numbers you land on when skip counting by 6, starting at 36 for 3 terms.
Predict the term number for the skip count by 3s and the term number for the skip count by 6s.
Record your thoughts on the following questions:
- What patterns have you found?
- Are there any connections or similarities between the 3s and 6s when you skip count?
- Were your predictions correct? Why or why not?
Click the ‘Reveal’ button to check your answer.
Action
Predicting geometric patterns
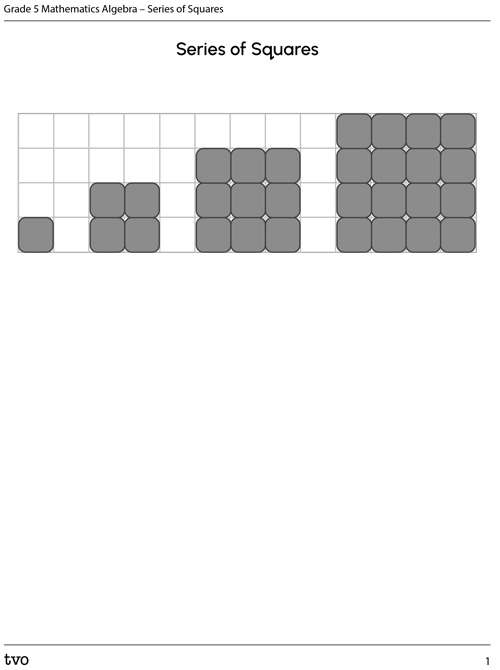
Explore the following pattern:
What kind of pattern is shown? What’s the pattern rule?
Extend the pattern to show the next 3 terms.
You can use the following fillable and printable Series of Squares document to record your answers. You may also use a voice recorder and describe the patterns.
Did you recognize a growing pattern?
Click the ‘Reveal’ button to check your answer.
The next 3 terms of the pattern would be

How does the way the patterns were described relate to square numbers? 1, 4, 9, 16, 25, 36, and 49 are called square numbers.
The pattern rule is to multiply the term number by itself
What term number would have 100 tiles?
Click the ‘Reveal’ button to check your answer.
Consider the following pattern. What kind of pattern is shown? Extend the pattern to show the next 3 terms. What’s the pattern rule?

You can use the following fillable and printable Series of Circles document to record your answers. You may also use a voice recorder and describe the patterns.
What would the term number be when there is only 1 circle left? How do you know?
Click the ‘Reveal’ button to check your answer.
The term number for when only 1 circle is left would be 8. I know because I extended the pattern.
Your turn
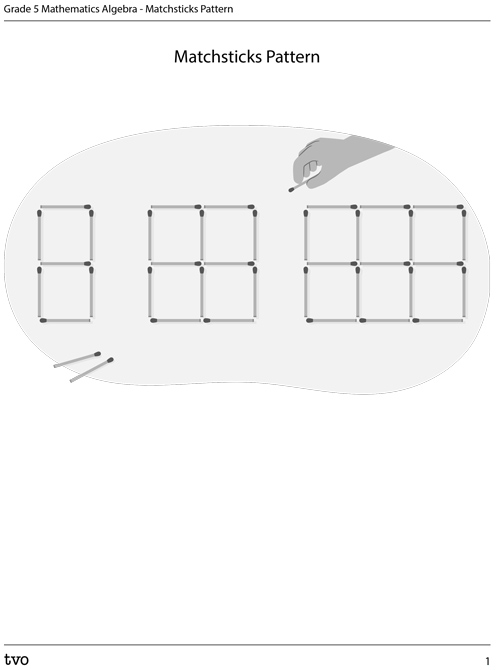
Consider the following match sticks pattern:
3 sets of matchsticks squares: Set 1 has 7 matchsticks that form 2 squares that are connected to each other forming a rectangle that is 1 matchstick by 2 matchsticks, Set 2 has 12 matchsticks that form 4 squares that connected together form 1 large square, Set 3 has 17 matchsticks that form 6 squares that when connected to each other form a large rectangle with a width of 2 matchsticks and length of 3 matchsticks.
How many matchsticks are in the first shape?
How many more are needed for the second shape?
What kind of pattern is shown? How do you know?
Extend the pattern to show at the next 3 patterns.
You can use the following fillable and printable Matchsticks Pattern document to record your answers. You may also use a voice recorder and describe the patterns.
What’s the pattern rule?
How many match sticks are needed for the 10th term? How do you know?
Click the ‘Reveal’ button to check your answer.
There are 7 matchsticks in the first shape. 5 more are needed for the second shape.
It is a growing pattern. I know because it’s getting bigger.
The pattern rule is start at 7 match sticks and add 5 each time.
Or Term #
Number of Matchsticks
The 10th term needs 52 matchsticks
Predicting numeric patterns
A pattern starts at 63 and subtracts 9 each time. The first 3 terms after are 54, 45, and 36. At what term would the value be less than 20? How do you know?
Let’s extend the pattern and find out!
63, 54, 45, 36, 27, 18. The 6th term! This is a shrinking pattern.
Extend the following pattern to find the next 3 terms.
7, 11, 15, 19, 23, (Blank), (Blank), (Blank)
What term number would have the value of 43?
Click the ‘Reveal’ button to check your answer.
Your turn
Extend the following pattern to find the next 3 terms.
100, 90, 80, (Blank), (Blank), (Blank)
What term number would have the value of 10? How do you know?
Click the ‘Reveal’ button to check your answer.
The next three terms would be 70, 60, 50. I know because the rule is to subtract 10 each time.
The tenth term will be the number 10. I know because each term is the next lower multiple of 10. If the first was 100 then the 10th will be 10.
Consolidation
Pattern of table arrangements
A school committee is planning a celebration.
There are 250 people coming to a special event at the school.
The tables and chairs are being arranged in a specific pattern.
The space can hold no more than ten table and chair arrangements.
Will there be enough seating for the 250 people who are coming?
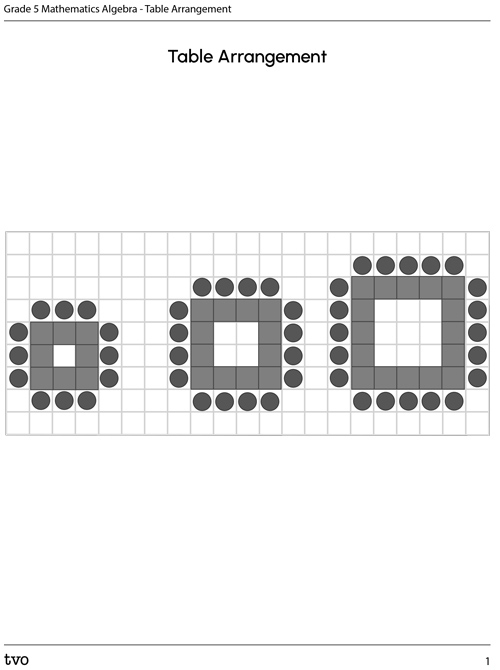
The first three table arrangements have been done for you.
There are three table and chair arrangements shown. In the first one, the 8 tables are arranged in a 3 by 3 square and there are 12 chairs around them. In the second arrangement, the 12 tables are arranged in a 4 by 4 square and there are 16 chairs around them. In the third arrangement, the 16 tables are arranged in a 5 by 5 square and there are 20 chairs around them.
You can use the following fillable and printable Table Arrangement document to record your answers. You may also use a voice recorder and describe the patterns.
What is the pattern rule for the number of tables? What is the pattern rule for the number of chairs?
Justify your reasoning around whether the venue will hold the 250 people coming.
Reflection
As you read through these descriptions, which sentence best describes how you are feeling about your understanding of this learning activity? Press the button that is beside this sentence.
I feel...
Now, record your ideas using a voice recorder, speech-to-text, or writing tool.
Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new tab)