Variables

A little bit about variables:

• Algebraic expressions are a combination of variables, operations, and numbers, such as 3a and a + b.
• Letters are often used as variables, especially the letter x. It is important to know and recognize when it is being used as a variable.
• When choosing letters for variables, try to use letters that make sense, like s for side or h for height.

Can you think of examples for when we need to use a variable or variables?

Press ‘Answer’ to reveal when we need to use variables.

Answer

Press ‘Answer’ to reveal some variables we can consider.

Answer

Algebraic expressions

s + s + s is an example of an algebraic expression.

What could this expression represent?

Do you think 3 s could represent 3 sides, and this expression could represent the perimeter of a triangle?

To find the perimeter of a triangle, we would add up all of the sides. If it’s an equilateral triangle, where all sides are the same length, we would only need one variable.

We could use s to represent the unknown length of a side. We could say P = s + s + s or P = 3 × s.

How could you use this information to create a formula for the perimeter of a regular hexagon? We know it has 6 sides, and all sides are equal.

How could you use this information to create a formula for the perimeter of a square? We know it has 4 sides, and all sides are equal.

How about finding the formula for a rectangle? Are all sides equal? If not, how many variables do we need?

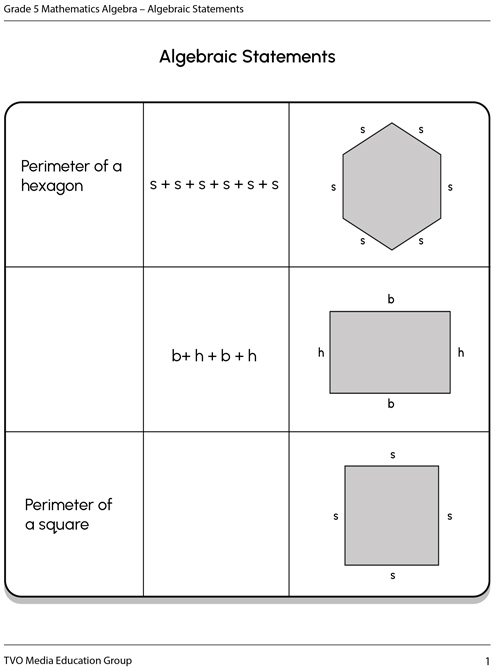
Fill in the Algebraic Statements table below with a possible solution. The first row has been completed for you.

You can use the following fillable and printable Algebraic Statements document to record your answers. You may also use your notebook or a voice recorder.

Press ‘Answer’ to reveal the missing solutions.

Answer

Sometimes algebraic statements will use the same variables many times.

s + s + s could be simplified as 3 s.

3 s means 3 × s or 3 multiplied by s. Are there other expressions in the table that could be simplified?

Did you find the perimeter of the hexagon, 6 s, or rectangle, 2(b+ h)?

Other examples include:

s + s + s + s + s = 5b

b+ h + b+ h = 2b+ 2h

Choose the correct algebraic expression that corresponds to the expressions given.

Considering the sides of different shapes

An artist is making a collage of three pictures and wants to put a border around each of them. Picture one is in the shape of a triangle, picture two a square, and picture three a hexagon. The sides of each shape are the same length, but they haven’t been measured exactly yet.

3 s + 4 s + 6 s = 13 s

The artist needs to purchase enough border for 13 side lengths.

1. What does this algebraic equation mean? Put it into words, using the information in the problem.
2. What would the artist need to know in order to know how much of a border is needed? What does 13 s mean?

Your turn

Three party planners are hosting an event together on the same day and invite their neighbours. Party planner one invites 3 people, Party planner two invites 2 people, and party planner three invites 10 people. They are going to buy some chips and dip, but are uncertain of the cost.

For this example, please note that c represents the cost per guest.

We could use the expression: 3c + 2c + 10c

1. What does this algebraic expression mean? Put it into words using the information in the problem.
2. What would the party planners need to know in order to know how much the total cost is? What does 15c mean?

Reflect

1. What is most important to remember when using variables?
2. How does grouping like terms help when simplifying an equation?

Reflection

As you read through these descriptions, which sentence best describes how you are feeling about your understanding of this learning activity? Press the button that is beside this sentence.

Now, record your ideas using a voice recorder, speech-to-text, or writing tool.