Codes and algorithms

Press Scratch(Opens in a new window) to explore the following code.

Description

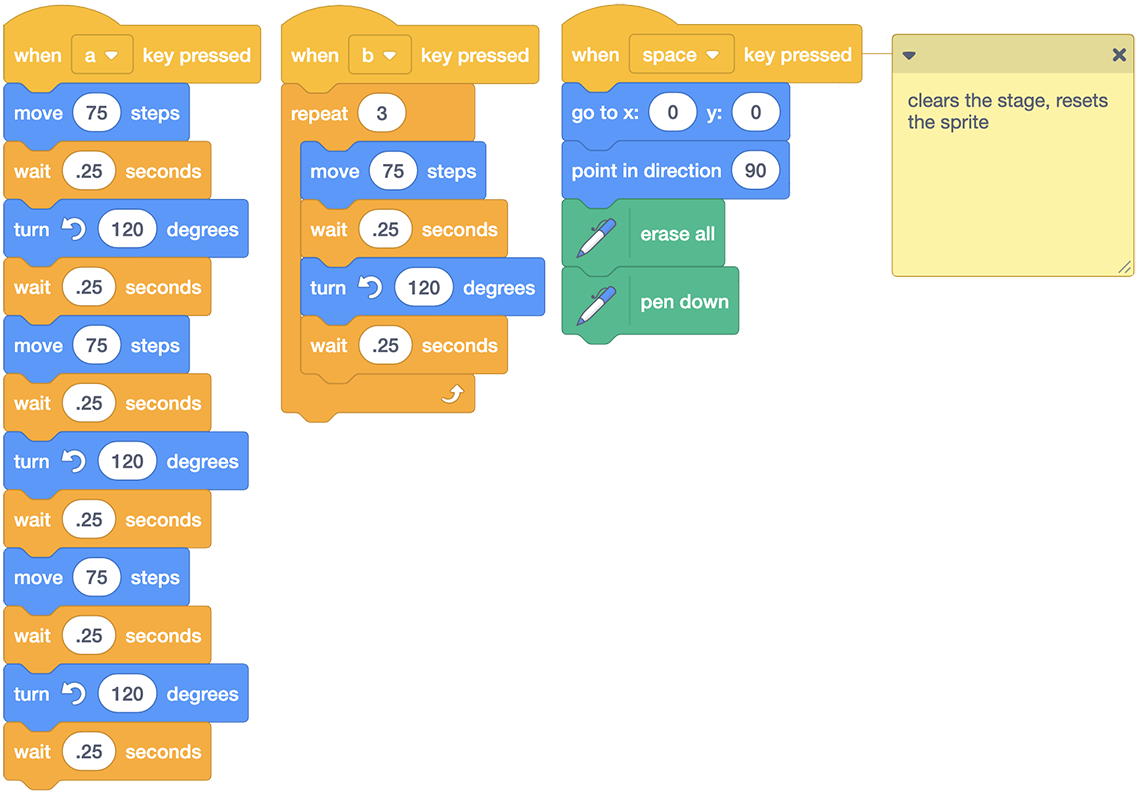
Below are the codes for the 2 algorithms a and b

When the a key is pressed

• move 75 steps
• wait 0.25 seconds
• turn 120 degrees
• wait 0.25 seconds
• move 75 steps
• wait 0.25 seconds
• turn 120 degrees
• wait 0.25 seconds
• move 75 steps
• wait 0.25 seconds
• turn 120 degrees
• wait 0.25 seconds

When the b key is pressed

• repeat 3
• move 75 steps
• wait 0.25 seconds
• tum 120 degrees
• wait 0.25 seconds

When the space key (which clears the stage and resets the sprite), is pressed

• go to x:0 y:0
• point in direction 90
• erase all
• pen down

• Press the spacebar. Then type the a key on the keyboard to execute – or run – the code for the first algorithm.

Algorithm:

An algorithm involves a sequence of step-by-step instructions for completing a task.

• What happens when this code is executed?
• Press the spacebar to reset the sprite and clear the stage.
• Type the b key on the keyboard to execute the code for the second algorithm.
• What happens when this code is executed?
• Compare the outputs of the two algorithms.
• The spacebar code resets the stage. Explain the difference between the code for the a and b algorithms.
• Which algorithm is more efficient – a or b? How do you know?

Press ‘The efficient algorithm’ to reveal which algorithm works in a more efficient manner and why.

The efficient algorithm

Let’s explore the following shapes

Now it’s time to draw our own two-dimensional shapes by writing a code that contains two different algorithms. When we write the code for two-dimensional shapes, we need to think about “moving around the shape.” To move around the shape, and turn, we are actually rotating the value of the exterior angle.

To calculate the individual exterior angles of a regular polygon such as a triangle, for example, take 360° and divide by the number of sides.

Explore the following diagram.

To determine the exterior angle of the triangle, take 360° and divide by the number of sides:

$\frac{\mathrm{360°}}{3}=120°$

Walk the shape of a triangle now.

Notice that at each turn, you will rotate 120°.

In the Minds On code, we turned 120°, which is the value of each exterior angle.

Connections

Connections

Notice that the interior angles of an equilateral triangle are each 60°.

120 + 60 add up to 180! The interior and exterior angles will always add up to 180° for a regular polygon. This is because together the two angles make a straight line which is 180°. Two angles that add up to 180° are called supplementary angles.

Let's explore the following regular pentagon

Previous Next

Calculate the exterior angle of a regular polygon. Remember to take 360° and divide it by the number of sides or vertices.

Did you get 72? That’s right!

Connections

Connections

What would the interior angles of the regular pentagon each be?

180 − ? = 72

? + 72 = 180

Did you get 108°? Great job! 108 + 72 = 180. Because they add up to 180°, the interior and exterior angles of a regular polygon are considered to be supplementary angles.

Let’s try two more shapes

• Calculate the exterior angle of a regular hexagon. Bonus: What is the value of the interior angles of a regular hexagon?

• Calculate the exterior angle of a regular octagon. Bonus: What is the value of the interior angles of a regular octagon?

Press ‘Answers’ to access the solutions to check your work.

Answers

Now that you know how to calculate the exterior angle, alter the code from the Minds On section to draw one of the shapes above – a pentagon, hexagon, or an octagon. Algorithm a will contain a code without a repeat, and Algorithm b will contain a more efficient code that incorporates a repeat.

Explore the following codes and algorithms:

For each of the following applications, indicate the output of the code for each algorithm. Also, explain which algorithm is more efficient, and why. Record your thoughts using a voice recorder, speech-to-text, or writing tool.

Student Success

Think-Pair-Share

If you’re not sure of the outcome, try recreating the algorithms using Scratch. Press Scratch(Opens in a new window) to access the website.

Note to teachers: See your teacher guide for collaboration tools, ideas and suggestions.

Application #1

Description

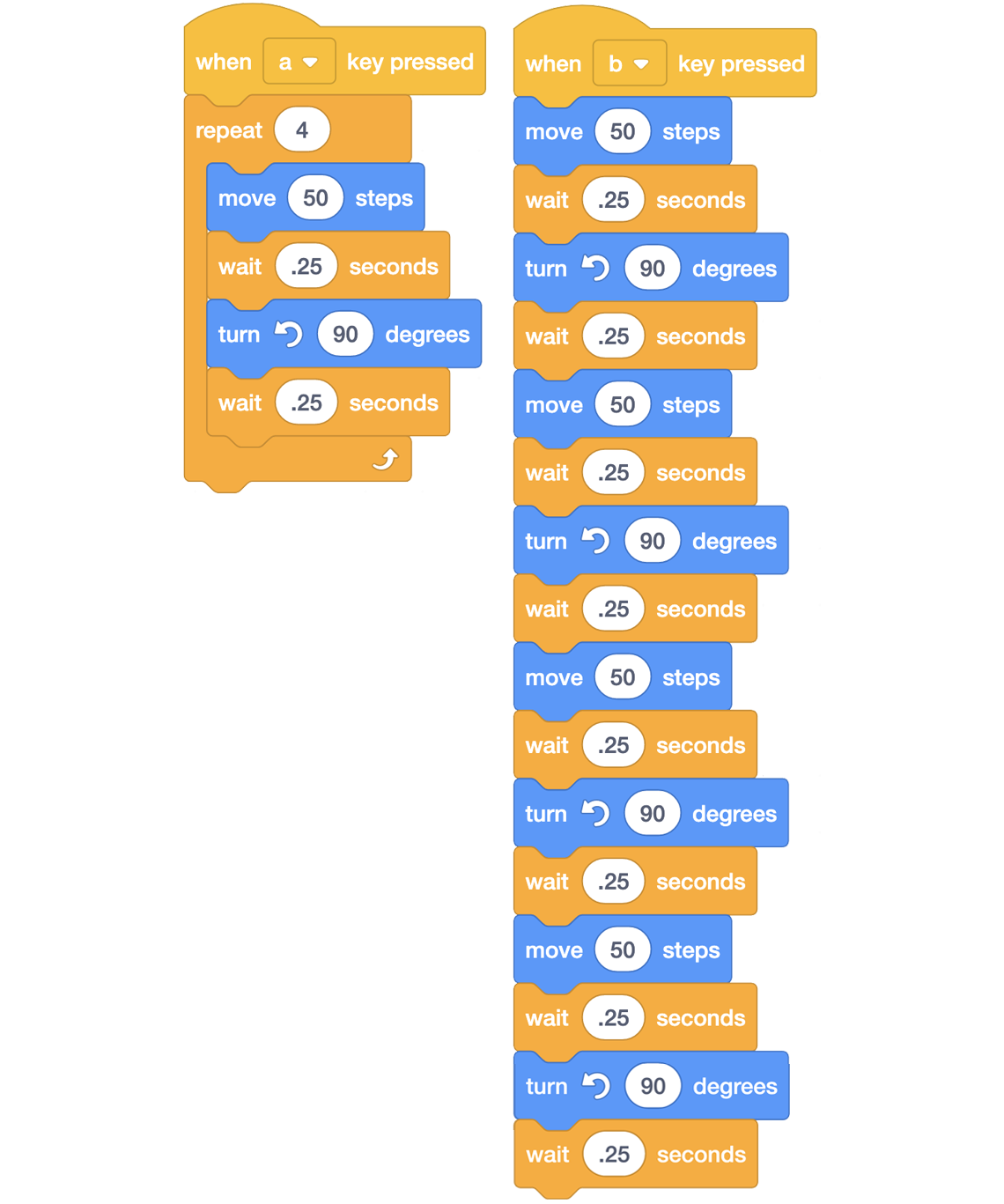
This is an image of a scratch code. It includes two algorithms a and b.

Below are the codes for the two algorithms a and b.

when the "a" key is pressed, the following steps will be repeated 4 times.

move 50 steps

wait 0.25 seconds

turn 90 degrees

wait 0.25 seconds

when the "b" key is pressed, the code sequence will go as follows:

move 50 seconds

wait 0.25 seconds

turn 90 degrees

wait 0.25 seconds

move 50 seconds

wait 0.25 seconds

turn 90 degrees

wait 0.25 seconds

move 50 seconds

wait 0.25 seconds

turn 90 degrees

wait 0.25 seconds

move 50 seconds

wait 0.25 seconds

turn 90 degrees

wait 0.25 seconds

• What is the output for each algorithm?
• Which algorithm is more efficient? A or b? How do you know? Explain your thoughts.

Application #2

Description

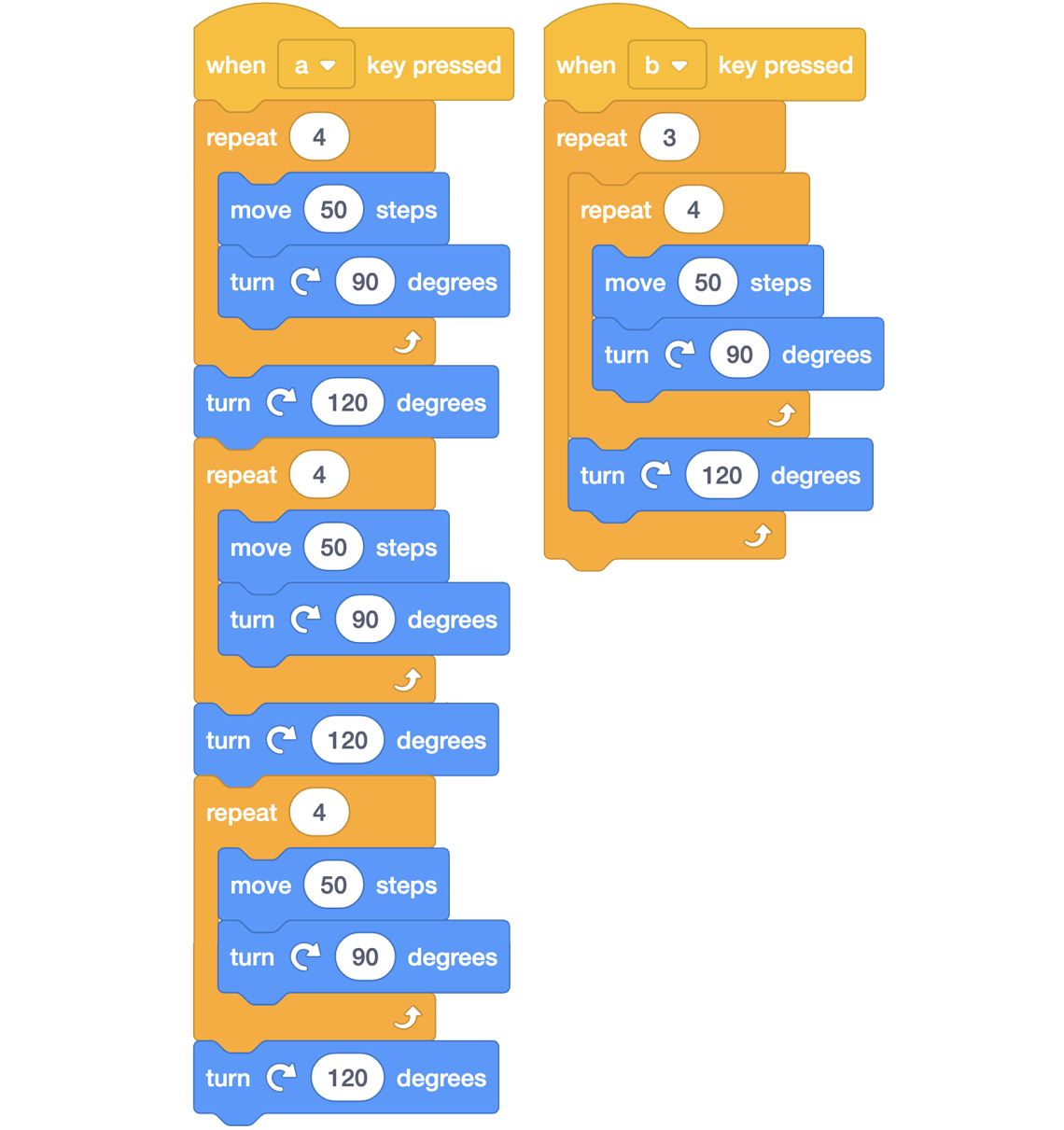
Below are the codes for the two algorithms a and b

when the "a" key is pressed, the following steps are repeated 4 times.

move 50 steps

turn 90 degrees

turn 120 degrees

repeat 4

move 50 steps

turn 90 degrees

turn 120 degrees

repeat 4

move 50 steps

turn 90 degrees

turn 120 degrees

when the "b" key is pressed, the code sequence is as follows:

repeat 3

repeat 4

move 50 steps

turn 90 degrees

turn 120 degrees

• What is the output for each algorithm?
• Which algorithm is more efficient? How do you know? Explain your thoughts.

Reflection

As you read through these descriptions, which sentence best describes how you are feeling about your understanding of this learning activity? Press the button that is beside this sentence.

I feel...

I have an excellent understanding of the concepts I have a very good understanding of the concepts I have some understanding but need to review some more my understanding of the concepts needs a lot more work

Now, record your ideas using a voice recorder, speech-to-text, or writing tool.

Connect with a TVO Mathify tutor