Minds On

Analyzing patterns

Examine the following algebraic equation:

2 x + 3 = y

What are the individual parts of this equation?

Let's explore the following terms together.

A fixed value. This is often a number (or sometimes a letter) on its own.

A symbol for a number we don’t know yet.

The number the term number is multiplied by.

Each repeat of a pattern or the position within a pattern. In a table of values, term number is shown in the left-hand column.

The total number of elements each time the pattern repeats. In a table of values, term value is shown in the right-hand column.

In the equation 2 x + 3 = y:

  • 2  is the multiplier
  • x  is the term number
  • 3  is the constant
  • y  is the term value

Both x  and y  are variables as they represent numbers we don’t know yet.

Now, use the terms as you consider the following pattern:

What is the constant, multiplier, and variable for this pattern?

Press ‘Answer’ to reveal the solution.

  • Constant = 3
  • Multiplier = 2
  • Variable = n

Think about the following questions. Record your thinking digitally, orally or in print.

  • Reflect on how the pattern relates to the ideas of constant and multiplier.
  • What is staying the same and what is changing respectively?

Action

Representing a pattern

Task 1

Let's practice with a pattern.

The pattern is: 2, 3, 4.

Complete the following 4 steps using this pattern as your guide.

Record your responses to each step digitally, orally or in print.

Step 1

Create a table of values and extend the pattern to 5 terms, including the 0 term. The column headings are: Term Number and Term Value.

Table of Values
Term number Term value
0
1 2
2 3
3 4
4
5

Complete Table of Values in your notebook or using the following fillable and printable document.

Press the ‘Activity’ button to access the Table of Values. 

Activity (Open PDF in a new window)

Step 2

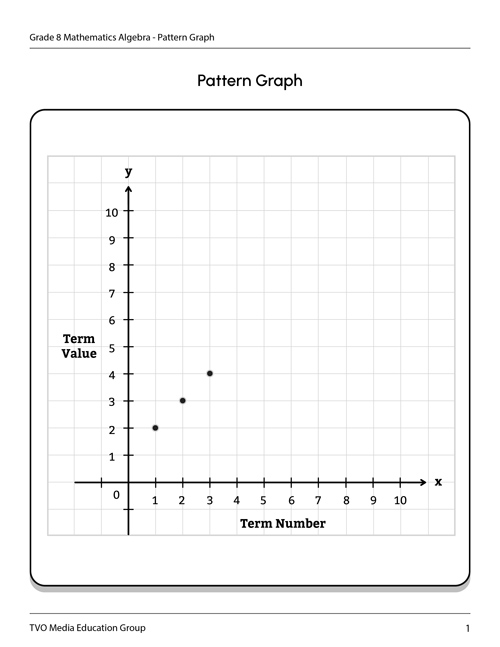
Create a graph of the pattern outlined in the table of values. When graphing patterns, the x-axis is the term number and the y-axis is the term value.

You may use the following graph for reference. Some of the coordinates have already been inputted for you. Copy the graph in your notebook, or use another method, and fill in the missing coordinates listed in your table of values.

You can also access a printable version of the Pattern Graph document to create your graph.

A graph with an x-axis labeled "Term Number" and a y-axis labeled "Term Value." Both axes have a scale that starts at 0 and goes up by ones to 10. The following points are plotted: (1,2), (2,3), and (3,4).

Complete Pattern Graph in your notebook or using the following printable document.

Pattern Graph

Press the Activity button to access the Pattern Graph.

Activity (Open PDF in a new tab)

Step 3

Describe the pattern rule in words by filling in the blanks.

Step 4

If you were to create the algebraic expression for the pattern, what might this be?

Press ‘Answer’ to compare your algebraic expression.

Term number + 1

Task 2

Step 1

Choose from the following 8 patterns.

Pattern 1 3, 4, 5
Pattern 2 5, 7, 9
Pattern 3 6, 10, 14
Pattern 4 6, 8, 10
Pattern 5 1, 4, 7
Pattern 6 5, 4, 3
Pattern 7 9, 6, 3
Pattern 8 1, 4, 9

*Note: Pattern 8 does not follow the typical pattern that we are used to!

Step 2

Describe the pattern you chose by:

  • inputting the pattern into a table of values
  • extending the pattern to 5 terms and include the 0 term
  • graphing the pattern
  • translating it into words
  • writing an algebraic equation

Use the steps in Task 1 as a guide.

Record your thinking digitally, orally, or in print. If you'd like, you can use the following fillable and printable Task 2 Worksheet document to guide you.

  1. Input your pattern into the following table of values. Extend the pattern to 5 terms and include the 0 term.
Task 2 Worksheet
Term number Term value
0
1
2
3
4
5
  1. Create a graph of your pattern. You can create your graph in your notebook or use another method of your choice.
  2. Translate your pattern into words.
  3. Write an algebraic equation for your pattern.

Complete Task 2 Worksheet in your notebook or using the following fillable and printable document.

Press the ‘Activity’ button to access the Task 2 Worksheet. 

Activity (Open PDF in a new window)

Task 3

Reflect on 2 of the following questions based on the patterns that you chose.

You can record your responses digitally, orally, or in print.

  • Compare pattern 1 and 3. What are their similarities and differences?
  • Compare pattern 2 and 4. What are their similarities and differences?
  • What makes pattern 5 unique?
  • What makes pattern 6 unique?
  • What makes pattern 7 and 8 different from the others?
  • What do you notice with the graphs when the multiplier is bigger?

Task 4

A student has a goal of reading a lot of books this year.

It is February 1st and they have already read 3 books.

For the rest of the year, they plan on reading 2 books a month.

Create a table of values that represents this situation or record a description of what you would do. You can record your thinking digitally, orally or in print.

How many books will be read by the end of May?

Consolidation

Mix and match

The following cards are pattern rules and tables, graphs, and visual representations for three patterns.

Sort the correct graphs, tables of values, and visual representations into 3 matching groups so that for each scenario there is one pattern rule, one graph, one table of values, and one visual representation.

If you’d like, you can use the following fillable and printable Mix and Match document to record your matches. You can also record your responses digitally, orally or in print, or using a method of your choice.

Table C is a table of values with the subheading “Pattern Rule: Subtract one from the term number.” The first column is labelled Term Number (x), and contains the following numbers, in order: 1, 2, 3, 4, 5, 6. The second column is labelled Term Value (y), and contains the following numbers, in order: 0, 1, 2, 3, 4, 5.

Graph B is a line graph and the scale on both axes goes from 0 to 10. There are 5 coordinates plotted on the graph: (1,0), (2,1), (3,2), (4,3), (5,4), (6,5).

Pattern B consists of three groups of blocks. The first term of the pattern is 1 block. The second term is 2 blocks. The third term is 3 blocks.

Table A is a table of values with the subheading “Pattern Rule: Add one to the term number.” The first column is labelled Term Number (x), and contains the following numbers, in order: 1, 2, 3, 4, 5, 6. The second column is labelled Term Value (y), and contains the following numbers, in order: 2, 3, 4, 5, 6, 7.

Graph C is a line graph and the scale on both axes goes from 0 to 20. There are 5 coordinates plotted on the graph: (1,4), (2,7), (3,10), (4,13), (5,16), (6,19).

Pattern A consists of four groups of blocks. The first term of the pattern is 4 blocks stacked vertically. The second term is 4 blocks stacked vertically with 3 blocks to the right stacked vertically, starting at the bottom block, for a total of 7 blocks. The third term is 4 blocks stacked vertically with 3 blocks to the right stacked vertically twice, starting at the bottom block for a total of 10 blocks. The fourth term is 4 blocks stacked vertically with 3 blocks to the right stacked vertically three times, starting at the bottom block, for a total of 13 blocks.

Table B is a table of values with the subheading “Pattern Rule: One plus three times a term number.” The first column is labelled Term Number (x), and contains the following numbers, in order: 1, 2, 3, 4, 5, 6. The second column is labelled Term Value (y), and contains the following numbers, in order: 4, 7, 10, 13, 16, 19.

Graph A is a line graph and the scale on both axes goes from 0 to 10. There are 5 coordinates plotted on the graph: (1,2), (2,3), (3,4), (4,5), and (6,7).

Pattern C consists of four towers of blocks. The first term of the pattern is 2 blocks stacked vertically. The second term is 3 blocks stacked vertically. The third term is 4 blocks stacked vertically. The fourth term is 5 blocks stacked vertically.
Mix and Match

Press the Activity button to access the Mix and Match.

Activity (Open PDF in a new tab)

Review what you've learned

Answer the following questions:

  • Which group was easiest to match together? Why?
  • How do you know you matched the groups correctly?

Reflection

As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.

I feel…

Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.

When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.