Minds On

Likely or unlikely?

What is the probability that the following events will occur?

For each event, select the corresponding level of probability.

Brainstorm

Consider the following

  • How could a probability line help you?
  • Does the outcome of each event depend on other events/outcomes?

Throughout this learning activity, you can record your ideas digitally, orally, or in print.

Action

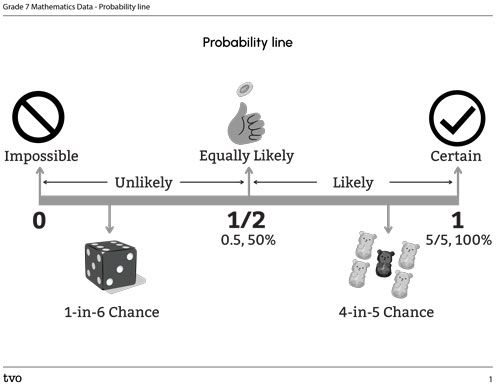
Probability Line

Probability refers to the likelihood of an event occurring – that’s to say, how likely or unlikely it is that the event will take place.

The probability line is a tool that can help us represent the probability of an event happening. The following line shows a continuum from zero to one.


You may find it convenient to refer to the probability line at various points in the learning activity. Press the thumbnail image to download the probability line.

Probability Line

Press the Activity button to access the Probability Line.

Activity (Open PDF in a new tab)

Activity 1

Consider where the following events would appear on the probability line.

For each event, select the corresponding level of probability.

Activity 2

We can assign percentages to the terms “likely” and “unlikely.”

For each sentence, select the missing word.

Expressing probability

There are different ways to express probability:

  • as a percentage, e.g., 50%
  • as a fraction, e.g., ½
  • as a decimal, e.g., 0.5

This table shows some more examples:

Event

Likely or unlikely?

Probability (as a fraction, decimal, and percent)

A game show has four prizes numbered 1 − 4. What is the likelihood of landing on 1, 2, or 3?

Likely

3 4 , 0.75, 75%

A bag contains 4 differently shaped tiles (3 triangles, 1 square). What is the likelihood that you will pick the square tile from the bag?

Unlikely

 1 4 ,0.25, 25%

Independent events

An independent event is one that is not affected by other events. If you flip a coin, you have an equal chance of getting heads or tails. This is true every time you flip the coin. Each flip is an independent event.

Press ‘Marbles and erasers’ to further explore the idea of independent events.

Let’s say a bag contains three marbles and three erasers. You have an equal chance of picking a marble or an eraser. Let’s say you pick a marble on your first try. If you replace the marble and then reach into the bag again, you still have the same probability of choosing a marble. Each of these draws is independent and has no impact on the next turn. A bag containing three marbles and three erasers

Thought experiment 1: Weather

To explore this concept further, imagine a game in which you press a button to randomly reveal one of seven kinds of weather: Sunny, Cloudy, Overcast, Rain, Drizzle, Snow, and Stormy. Each time you press the button, any of the seven types could be revealed.

Complete the Weather 1 table in your notebook or use the following fillable and printable document. If you prefer, use another method to record your ideas.

Weather 1

Sunny Weather: When you press the button, what is the probability of revealing sunny weather? Express the probability in the following ways:
Fraction: Decimal: Percent:
Where does this event fall on the probability line?
If you press the button 10 times in a row, does the probability change?

Not-Sunny Weather: When you press the button, what is the probability of revealing weather that is NOT sunny? Express the probability in the following ways:
Fraction: Decimal: Percent:
Where does this event fall on the probability line?
If you press the button 10 times in a row, does the probability change?
BONUS: What is another example of a dependent event?

Press the ‘Activity’ button to access Weather 1. 

Activity(Open PDF in a new window)

Press ‘Answers’ to reveal the solution.

Weather 1

Sunny Weather: When you press the button, what is the probability of revealing sunny weather? Express the probability in the following ways:
Fraction:
1 7 		Decimal:
0.14		 Percent:
14%
Where does this event fall on the probability line?

Near the word unlikely
If you press the button 10 times in a row, does the probability change?

No. The chance of getting not-sunny would still be 6 7

Not-Sunny Weather: When you press the button, what is the probability of revealing weather that is NOT sunny? Express the probability in the following ways:
Fraction:
6 7 		Decimal:
0.86		 Percent:
86%
Where does this event fall on the probability line?

This is very likely.
If you press the button 10 times in a row, does the probability change?

No. The chance of getting not-sunny would still be 6 7
BONUS: What is another example of a dependent event?

Dependent events

A dependent event is one that is affected by a previous event. That’s to say, the outcome of the first event affects the outcome of the second (dependent) event. For example, each time a card is drawn from a deck of cards without being replaced, the probability of selecting a specific card from the deck changes.

Press ‘Marbles and erasers’ to further explore the idea of dependent events.

Let’s return to the bag containing three marbles and three erasers. You have an equal chance of picking a marble or an eraser. On your first try, you pick an eraser, but you don’t put it back in the bag. The probability of drawing an eraser from the bag on your next turn has now changed as there are only two erasers remaining in the bag. The outcome of the first draw has affected the outcome of the second draw. The second draw is therefore a dependent event.

A bag containing three marbles and two erasers. An eraser which has been drawn from the bag sits beside it.

Thought experiment 2: Weather

Let’s go back to the game in which you press a button to randomly reveal one of seven kinds of weather: Sunny, Cloudy, Overcast, Rain, Drizzle, Snow, and Stormy. There’s a difference this time: each time you reveal one type of weather, it is removed from the game. That means that each turn is dependent on what happened in the previous turn. The types of weather that remain have changed because one has been removed.

Complete the Weather 2 table in your notebook or use the following fillable and printable document. If you prefer, use another method to record your ideas.

Weather 2

Not-Sunny Weather: On your first turn, you have eliminated sunny weather. Now it’s your second turn. When you press the button, what is the probability of revealing weather that is NOT sunny? Express the probability in the following ways:
Fraction: Decimal: Percent:
Where does this event fall on the probability line?
If you press the button 10 times in a row, does the probability change?
BONUS: What is another example of an independent event?

Press the ‘Activity’ button to access Weather 2. 

Activity(Open PDF in a new window)

Consolidation

Independent or dependent?

Press the terms below to refresh your memory about the definitions.

An event is independent if its outcome is not affected by another event. For example, these two events are independent: rolling a 6 on a number cube and drawing a 5 from a deck of cards.

An event is dependent if its outcome is affected by a previous event. For example, each time a card is drawn from a deck of cards without being replaced, the probability of selecting a specific card changes. Each subsequent draw is dependent.

Activity: You create the scenarios!

Select two of the following four situations to explore.

  • You have five shapes: three cubes and two triangles.
  • You have twenty-six letters.
  • You have a list of thirty movies.
  • You have one coin and two dice.

Complete Exploring Two Situations in your notebook or use the following fillable and printable document. If you prefer, use another method to record your ideas.

Exploring Two Situations

SITUATION 1: (Place a check mark besides one of the following choices)
Create a situation that involves independent events. Explain why the events are independent.

SITUATION 2:(Place a check mark besides one of the following choices)

Create a situation that involves dependent events. Explain why the events are dependent.
Explain how the probabilities differ in the two situations.

Press the ‘Activity’ button to access the Exploring Two Situations.

Activity (Open PDF in a new window)

Reflection

As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.

I feel…

Now, expand on your ideas by recording your thoughts using a voice recorder, text-to-speech, or writing tool.

When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.

Press ‘Discover More’ to extend your skills.

Complete Analyzing Tree Diagrams in your notebook or use the following fillable and printable document. If you prefer, use another method to record your ideas.

Analyzing Tree Diagrams
How are the tree diagrams similar? How are they different?
Which tree diagram illustrates drawing two items independently from each other? (independent events)
Which one illustrates drawing two items where the outcome of the second draw depends on the first? (dependent events)
Determine the probability of drawing two rocks in the independent-event scenario.
Compare this to the probability of drawing two rocks in the dependent-event scenario.

Press the ‘Activity’ button to access Analyzing Tree Diagrams. Activity(Open PDF in a new window)

Connect with a TVO Mathify tutor

Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.

TVO Mathify (Opens in new window)