Minds On
Possible outcomes
When determining the probability of an event, we divide the number of favourable outcomes (the one that we are watching for) by the total number of possible outcomes.
What are the possible outcomes when flipping a coin? The coin is double sided, one side is heads and the other is tails.
What is the probability of getting tails?
Throughout this learning activity, you can record your ideas digitally, orally, or in print.

Determine the possible outcomes for the following objects.
If I had a six-sided object labelled with numbers one through six, what are the possible outcomes?

Brainstorm
Possible outcomes
If two sports teams are playing, what are the possible outcomes of the game if it is not possible to end in a tie? How do you know?
What about the outcomes for the weather during the winter? How about the weather at any point during the year?
What about having a deck of cards or a button that displays the same information as a deck of cards?

Action
Task 1: Theoretical and experimental probability
Let’s learn about theoretical and experimental probability. Teacher Sarah is going to introduce the two types of probability in the following video.
Theoretical probability is the mathematical calculation of the chances that an event will happen in theory. If all outcomes are equally likely, it is calculated as the number of favourable outcomes divided by the total number of possible outcomes.
For example, if two teams play a sport against each other 10 times (and we assume that there will not be a tie), we expect Team A to win five games and Team B to win five games because the probability of each team winning is 50%, , or 0.5 as both teams have equal chances to win.
The theoretical probability is determined by dividing the number of favourable (desired) outcomes by the total number of possible outcomes.
Experimental probability is the measurement of the likelihood of an event happening based on the results gathered from running many trials of an experiment.
For example, we conducted an experiment by observing two teams play 10 times (and we assume that there will not be a tie). We record four wins for Team A and six wins for Team B. The experimental probability of Team A winning is and the experimental probability of Team B winning is
Task 2: Five option probability
Imagine a spinner divided into five equal sections or an electronic game that provides the same options. The event is the spinner landing on one of the five equal sections.

- Determine the theoretical probability of each of the five possible events occurring.
- Determine the theoretical probability of each event occurring if you were to play 50 times.
- Would you expect the theoretical and experimental probability to be the same or different? Why do you think this is the case?
Press ‘Answers’ to reveal the solution.
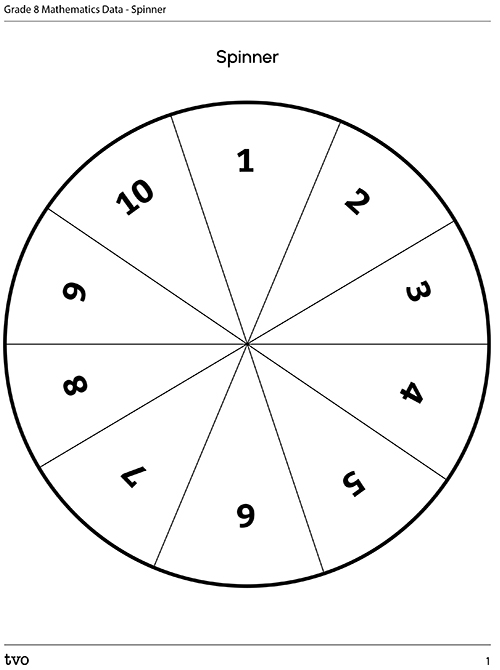
Task 3: Ten-option probability
Imagine a spinner divided into ten equal sections or an electronic game that displays the same options. The event is the spinner landing on one of the ten equal sections.

Press ‘Answer’ to check the answer to each question.
Determine the theoretical probability of each of the ten events occurring.
Event of spinner landing on section labeled 5.
Event of spinner landing on a multiple of 3.
Event of spinner landing on a prime number.
Event of spinner landing on 11.
Using the following Ten-Option Spinner, spin the spinner ten times. You can put a pencil or pen at the centre point and use a paper clip as the spinner. Record your results.Now, determine the experimental probability of each event occurring.
Consolidation
Design your own game

Design your own game and determine what the theoretical probability versus the experimental probability will be if you were to try the game 50 times.
You can create a spinner, a digital/electronic game which involves pressing a button to reveal the outcome, or another probability game of your choice.
- Compare the theoretical probability and the experimental probability for each of the outcomes.
- Why might there be an inconsistency between the theoretical and experimental probabilities?
Reflection
As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.
I feel…
Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.
When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.
Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in new window)