Minds On
Making sense of cents
We are learning about a new place value in the place value chart called tenths.
Let’s learn more about tenths. Access the following episode of Homework Zone called “What’s a Tenth?” for an explanation about tenths.
The dot (•) is the decimal. Whenever when we come across the decimal (•) and a number in the tenths column, it means that there is more than a whole number (ones, tens, hundreds, thousands, ten thousand) but just a little more.
Think of some real-life situations where you come across decimals with tenths.
Action
Part 1: A tenth of a pizza versus ten pizzas
One tenth can mean you have one slice of a pizza that is cut into tenths (ten equal pieces).

If we have 2 slices of this pizza, we have 2 tenths.
Complete the following fillable and printable document “Pizza Slices Chart” for a pizza cut into 10 equal slices. Record the number of slices as tenths and as decimals. You can also complete this activity in your notebook.
| Number of slices | Number of tenths | Decimal |
|---|---|---|
| 1 | 1 tenth | 0.1 or (0.10) |
| 2 | 2 tenths | 0.2 or (0.20) |
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 |
Press the ‘Activity’ button to access Pizza Slices Chart.
Notice the “th” at the end – a tenth this is very different than ten.
One tenth can mean you have one pizza that is cut into tenths (ten equal pieces) while ten pizzas means you have 10 whole pizzas.

Or, if we have a chocolate bar that has tenths (10 equal smaller pieces to break off), it is very different than having ten WHOLE chocolate bars.


When we split or divide the whole into ten equal parts, then each equal part is a called a tenth.
In a 10-card set, each individual card makes up a tenth of the set, even though each card is a whole card in itself.
Similarly, for a soccer team playing on the field not including the goalie, there are 10 soccer players active in a soccer game. Each soccer player on the field makes up 1 tenth of the players defending and attacking in the current game (again, excluding the goalie).

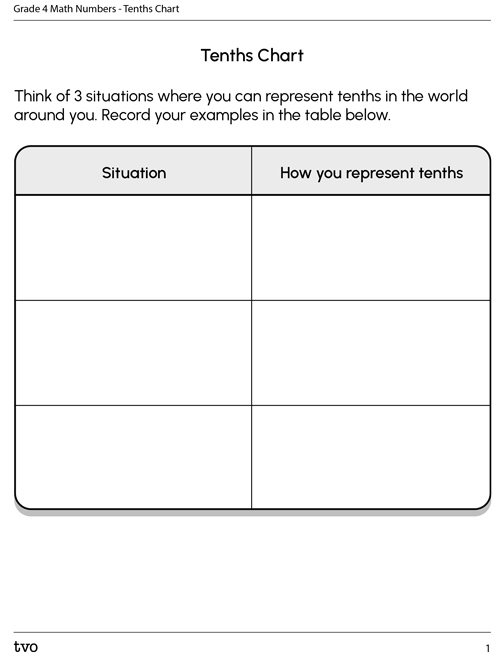
Think of 3 other situations where you can represent tenths in the world around you. Record your examples in the following fillable and printable document “Tenths Chart.” You can also complete this activity in your notebook.
Share your situations with a partner, if possible. Did you have any situations that were similar?
Part 2: Using money to count tenths
Now, let’s return to tenths when representing money amounts.
If we take 1 loonie ($1.00) or 1 dollar and divide it into TEN equal parts, then each tenth is a dime or 10 cents.

Similarly, if we take $10.00 and divide it into TEN equal parts then each tenth is a loonie or $1.00.
If we take $100.00 and divide it into TEN equal parts, then how much is a tenth of $100.00?
Part 3: Tenths as words
The dot symbol (•) is the decimal. Whenever when we come across the decimal (•) we say, “AND”
For example, when we read the following decimal number in word form:
29.2
we say,
“twenty-nine AND two tenths.”
If we have a larger number such as:
9,829.2
we say,
“nine-thousand eight-hundred twenty-nine AND two tenths.”
Tenths in expanded form
The expanded form for 19.2 is 10 + 9 + 0.2
19.2 = 10 + 9 + 0.2
The expanded form for 9,829.2 is 9,000 + 800 + 20 + 9 + 0.2
9,829.2 = 9,000 + 800 + 20 + 9 + 0.2
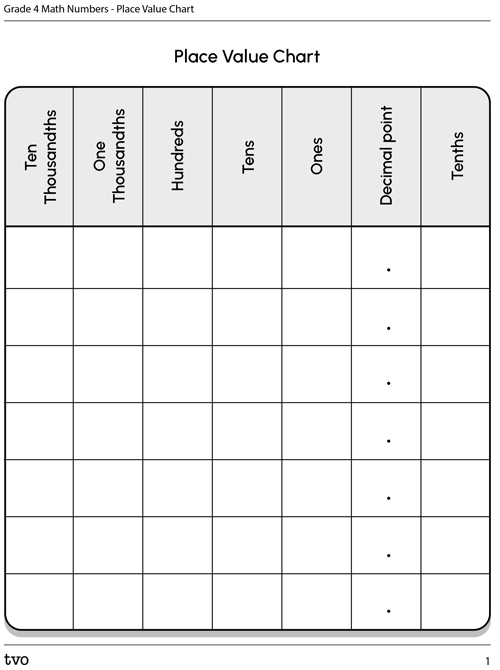
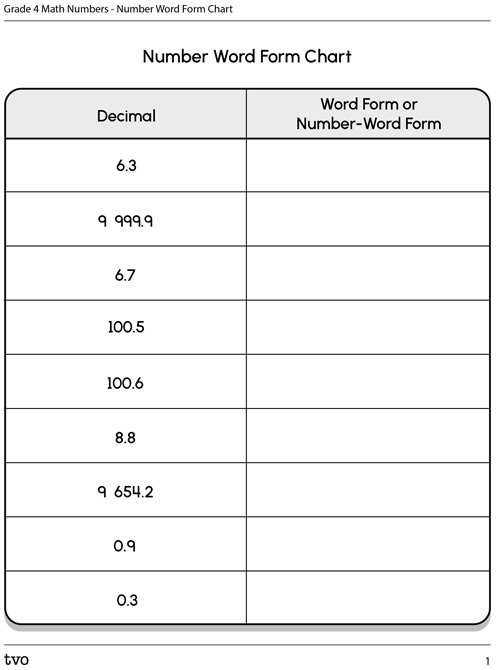
Let’s try it out! Complete the following fillable and printable “Word Form Chart.” Also, use the printable and fillable “Place Value Chart” to represent the numbers in expanded form. You can also complete this activity in your notebook.
Practice reading the numbers making sure you read the decimal (•) using the word “AND.”
Ordering tenths
Compare the digits in the tenths place value.
6.3 and 6.7
Since 7 tenths is larger than 3 tenths, 6.7 > 6.3
Practice time
The fastest person to run the 100 metres race at the Olympics is considered the fastest person to run on Earth. On April 6, 1,896 the first qualifying race for the 100 metres kicked off the first Olympic Games event of the modern era.
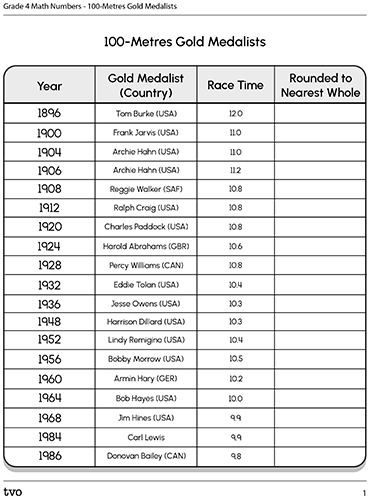
Consider some of these Olympic Gold medal race times for the 100 metres race from 1,896 to 1,996 (in seconds):
9.8 10.2 10.8 10.3 12.0 10.4 10.5 11.0 9.9 10.6 10.0
Order these race times from fastest to slowest.
Then order these race times from largest to smallest.
Task 2: Rounding to the nearest whole number
Access the following episode of Homework Zone to review rounding up and rounding down.
Now let’s practice. Complete the following fillable and printable “100-Metres Gold Medalists” chart by rounding each of the 100 metres winning times to the nearest whole number.
Consolidation
Practice
It is now time for you to demonstrate all that you have learned about tenths.
Complete the activities from group 1 and 2. Be sure that you are expressing what you know in a way that works best for you.
Group 1
Let’s think back to when we worked with money as tenths. Can you create a situation where you represent different amounts of money that include parts of a dollar? For example,
$2.50 = $2.00 + 5 dimes ($2.00 + $0.10 + $0.10 + $0.10 + $0.10 + $0.10)
$8.10 = $4.00 + $4.00 + 1 dime ($4.00 + $4.00 + $0.10)

Group 2
Think of a situation where you can create 5 numbers that include tenths (e.g. 4.7)
For those 5 numbers, do the following:
- order the numbers from greatest to least
- round each number to the nearest whole number
- write each number in expanded and word form
Reflection
As you read through these descriptions, which sentence best describes how you are feeling about your understanding of this learning activity? Press the button that is beside this sentence.
I feel...
Now, record your ideas using a voice recorder, speech-to-text, or writing tool.
Press 'Discover More' to extend your skills.
Discover MoreAmazing animal speeds

In 2012, Sarah, an 11-year-old cheetah from the Cincinnati Zoo was timed covering 100 metres in 5.9 seconds. Choose the fastest Olympic time in the “100-Metres Gold Medalists” table from the "Action" section. Write a math sentence and calculate how much faster Sarah ran.
Research the fastest Olympic time in 2012 (and who). Write a math sentence to find the difference between the fastest cheetah and the fastest Olympic time of 2012. Calculate how much faster Sarah ran.
Research 3-5 other fast-moving animals (four-legged, water animals or winged animals) and compare their speeds to the most recent 100 metres Olympic gold medalist time. This means: find the difference between each animal’s time and the most recent 100 metres Olympic gold medalist time.
If animals can move so much faster than humans, do you think it is fair that some of them live in zoos with limited space compared to their natural habitat in the wild? Explain your answer.
Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new tab)