Minds On
Decimals and fractions
Every decimal that ends can be written as a fraction:
| Decimal: | Fraction: |
|---|---|
| 0.25 | |
| 0.0041 | |
| 31.7 |
These types of decimal numbers are also called terminating decimals.
Terminating decimal
A decimal number that has a finite number of digits.
Question: Using the previous 'decimals and fractions' table with the examples, describe how to convert a decimal number that ends into a fraction.

Decimals that repeat can also be written as fractions. A repeating decimal, also called a recurring decimal, is a number whose decimal representation eventually becomes periodic or has the same sequence of digits repeats indefinitely, e.g., 2.613613613. Construct a list of examples of fractions that you know are repeating decimals. Complete Repeating Decimal Fractions in your notebook or use the following fillable document.
Notation Alert: Sometimes to save space, repeating decimals are written using a “bar” over the section that is repeating. For example:
For each of the following three repeating decimal numbers, write either the short-hand notation (using the bar) or the expanded notation (demonstrating which part is repeating)
Record your response in the space provided.
| Decimal in Short-Hand Notation | Decimal in Expanded Notation |
|---|---|
If you would like, you can complete this activity using TVO Mathify. You can also use your notebook or the fillable document.
Press the ‘TVO Mathify' button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in new window) Activity (Open PDF in a new window)Action
Rational numbers
Numbers that are a:
- terminating decimal
- repeating decimal
- whole number, or
- integer
are called rational numbers.

Rational vs irrational numbers
-
A rational number is any number that can be written as a fraction.
- Pause and Think: How can a whole number, say 6, be written as a fraction?
- An irrational number is any number that cannot be written as a fraction.
Expand the list in the following fillable and printable "Examples of Rational and Irrational Numbers" chart.

Press the Activity button to access Examples of Rational and Irrational Numbers.
Activity (Open PDF in a new tab)It does not seem like there are a whole lot of irrational numbers…or are there?

Task: Build your own irrational number
An irrational number is a decimal number that does not repeat and does not end.
- Start with any rational number, say 0.2
- How could we make it irrational using the definition? Discuss possible strategies with a partner or record your thinking. What strategies did you use to create the irrational number?
Since an irrational number is a decimal number that goes on forever, it must be expressed something like this.

If each space is filled by a random digit from 0-9 and you fill in the spaces forever, you will always create an irrational number. The … represents the list going on forever.
In your notebook, construct a collection of irrational numbers between the two numbers given here. Complete My Examples of Irrational Numbers in your notebook or use the following fillable document.

Press the Activity button to access My Examples of Irrational Numbers.
Activity (Open PDF in a new tab)Student Success
Think-Pair-Share
Think: Reflect on the following question:
- How many irrational numbers are there between 0 and 1?
Record your thinking in your notebook or in a recording.
If working with a partner, discuss your response.
Note to teachers: See your teacher guide for collaboration tools, ideas and suggestions.
The real numbers
We call the collection of all rational AND irrational numbers the real numbers.
Question: Use the following fillable and printable "Least to Greatest Real Numbers" document to order lists of real numbers from least to greatest.

Press the Activity button to access Least to Greatest Real Numbers.
Activity (Open PDF in a new tab)Question: Construct your own list of real numbers. Build it so that it is challenging to order from least to greatest. Pause and Think: How can you make it challenging? If possible, exchange your list with a partner and try to order the lists.
Consolidation
Rational or irrational?
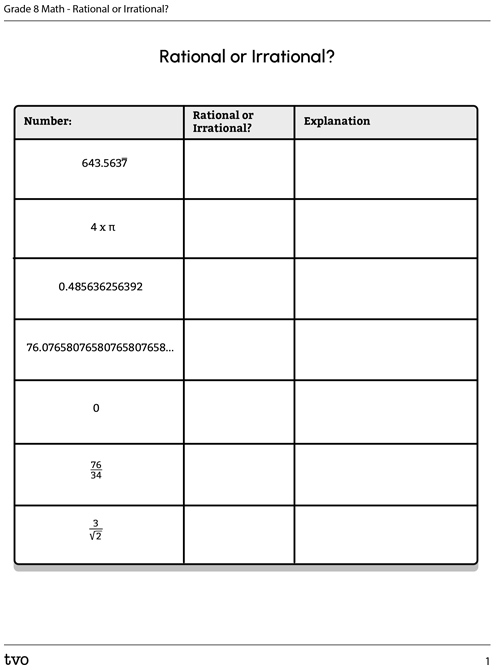
For each of the following real numbers listed in the fillable chart, state whether it is rational or irrational. Explain your reasoning for each number. Complete Rational or Irrational in your notebook or use the following fillable document.
Reflection questions
Suppose you make a calculation on a calculator and the number you get is a decimal number that fills the screen. The number is:
Can you say for certain whether this number is rational or irrational? Why or why not?
Consider each of the following questions carefully:
- How many whole numbers are there?
- How many integers are there?
- How many rational numbers are there?
- How many irrational numbers are there?
- How many real numbers are there?
- Was your answer different for any of the above questions? Why or why not?
Reflection
As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.
I feel...
Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.
When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.
Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in new window)