Numbers and architecture

Mathematics is used all the time in the field of architecture. Architects use numbers to build buildings, decide on what materials to use and how much they need for a structure. Being able understand and work with numbers is a very important part of an architects job. For example, creating blueprints for buildings and homes involves square root calculations.

Square roots of numbers

If you multiply the length of the square by the width of the square the product will be a square number.

A square number is the number we get after multiplying an integer (not a fraction) by itself. The symbol for square root is √.

To take the square root of a number is to find the side length of the square whose area is the original number.

For example, consider that $\sqrt{25}=5, \mathrm{since} 5\times 5=25.$

Let's practice. Use the side length of the following seven squares to find the square root.

If you would like, you can complete this activity using TVO Mathify. You can also use your notebook or the following fillable worksheet.

Practice using the square root

Let’s practice using the square root.

Task 1: Working with square roots

Only certain numbers, square numbers, have whole numbers as their square roots. It is helpful to know these, so here is a list of them.

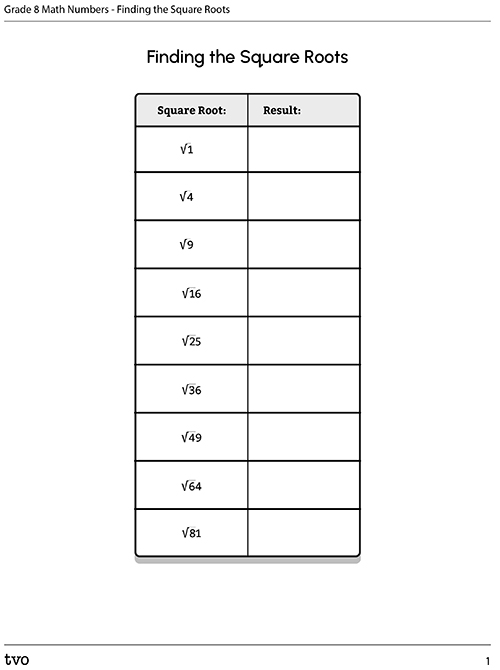
The following fillable and printable "Finding the Square Roots" document contains a list of square numbers. Fill in the missing blanks in the document.

Press the Activity button to access the Finding the Square Roots.

Activity (Open PDF in a new tab)

Question: Using any strategy you would like, calculate the following:

$$\begin{gathered} 9\times 4= \\ \sqrt{9}\times \sqrt{4}= \\ \sqrt{36}= \end{gathered}$$

Next:

$$\begin{gathered} 36\times 81= \\ \sqrt{36}\times \sqrt{81}= \\ \sqrt{\mathrm{2,916}}= \end{gathered}$$

What do these examples show us about the square root?

We can look at equivalent square roots in their lowest form. We can do this because of the rule that we saw in the 9 × 4 and 36 × 81 examples earlier.

$$\begin{gathered} \sqrt{45} \\ =\sqrt{9\times 5} \\ =\sqrt{9}\times \sqrt{5} \\ =3\times \sqrt{5} \\ =3\sqrt{5} \end{gathered}$$

Test Your Skills

Practice

Reduce the following square roots to their lowest form. Show all your steps.

$\sqrt{48}$

$\sqrt{180}$

$\sqrt{343}$

Working with square roots practice

For each of the following, break down the square root into its lowest form.

Think back to the common square roots we considered in the Mind’s On. Write an extended list for the squares of numbers 10 – 20.

Reflection questions

• Describe how you would estimate the number $\sqrt{80}$   without using a calculator.

Reflection

As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the correlating button once you have made your choice.

I feel...

I have an excellent understanding of the concepts I have a very good understanding of the concepts I have some understanding but need to review some more my understanding of the concepts needs a lot more work

Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.

When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.

Press ‘Discover More’ to extend your skills.

Part 1

Think back to when you first learned about numbers, counting, adding, and subtracting. At the time of learning these things, it may have felt like a lot to handle. Now, you are much more comfortable with counting, adding, and subtracting whole numbers and you know that there is much more to math than just this.

The same thing applies for complex numbers. There is a lot more to complex numbers than what we have learned. Here are some questions that you can research about complex numbers:

• How do you multiply? How do you divide?
• What about order of operations (BEDMAS) – how does this work for complex numbers?
• Why are complex numbers useful? What careers/fields of study use complex numbers?
• Are there more complex numbers or real numbers? Why?
• What kind of art has been created with the use of complex numbers?

Part 2

We have this relationship between multiplying, squaring a number, and the square root:

Multiplication The area of the square with side length 4	Squaring The area of the square with side length 4	Square Root The side of the square
$4\times 4$	$4^2$	$\sqrt{16}$

There is nothing stopping us from multiplying more than twice:

Multiplication	Cubing	Cubed Root
$4\times 4\times 4$	$4^3$	$\sqrt[3]{64}$

Question: What do each of the columns represent geometrically? (Hint: Taking the square root had to do with squares…)

In general, we could take any root of a number, not just the square root. Here are a few examples:

$$\begin{gathered} \sqrt[5]{32} \\ =2 \end{gathered}$$

$$\begin{gathered} \sqrt[6]{\mathrm{117,649}} \\ =7 \end{gathered}$$

$$\begin{gathered} \sqrt[3]{\mathrm{1,331}} \\ =11 \end{gathered}$$

Practice

Practice

Calculate the n-th root of each number. Try this without a calculator at first, though one may be required for some of these questions.

$\sqrt[3]{729}$

$\sqrt[4]{256}$

$\sqrt[3]{48}$

$\sqrt[5]{128}$

$\sqrt[10]{\mathrm{59,049}}$

$\sqrt[764]{1}$

Connect with a TVO Mathify tutor