Minds On
‘Cartesian’ questions
Explore the following description and image.
A Cartesian plane. There are 2 perpendicular number lines on a grid. The horizontal number line is labelled the x-axis and the vertical number line is labelled the y-axis. These two perpendicular number lines are both numbered from negative 5 through 5, from left to right, and from bottom to top. The lines intersect in the centre at (0, 0) and extend in all four directions to create a grid with 4 quadrants.
Think about the following questions. Record your ideas in a notebook or a method of your choice.
- What do you notice and wonder about the image?
- How can the image be used?
- Have you used something like this before?
- How is this similar and different than a grid?
Action
What is a Cartesian plane?
The Cartesian plane uses two perpendicular number lines to describe locations on a grid.
The x-axis is a horizontal number line and the y-axis is a vertical number line.
These two number lines intersect at the origin, (0, 0).
These two perpendicular number lines create four quadrants.
The number lines on the Cartesian plane extend infinitely in all four directions.
You can explore these features on the following example of a Cartesian plane.
There are 2 perpendicular number lines labelled as the x-and y-axis that intersect at (0, 0). The x-axis is a horizontal number line, and the y-axis is a vertical number line. These two perpendicular number lines create a grid with 4 quadrants and the number lines on the x- and y- axis extend in all four directions.
What are the sections of a Cartesian plane?
The different sections of a Cartesian plane are called quadrants.
There are four quadrants created by the two perpendicular lines.
Quadrant 1 is in the top right, quadrant 2 is in the top left, quadrant 3 is in the bottom left and quadrant 4 is in the bottom right. The quadrants include both positive and negative numbers, which are centred by the origin, (0, 0).
Explore the following image of a Cartesian plane. All four quadrants are labelled.
A Cartesian plane with labels. There are 2 perpendicular number lines on a grid. The horizontal number line is labelled the x-axis and the vertical number line is labelled the y-axis. These two perpendicular number lines are both numbered from negative 10 through 10, from left to right, and from bottom to top. The lines intersect in the centre at (0, 0) and extend in all four directions to create a grid with 4 quadrants. The top right quadrant is labelled “Quadrant 1” and includes all the positive numbers that appear along the x- and y-axes. The top left quadrant is labelled “Quadrant 2” and includes the negative numbers that appear along the x-axis, and the positive numbers that appear along the y-axis. The bottom left quadrant is labelled “Quadrant 3” and includes all the negative numbers that appear along the x- and y-axes. Finally, the bottom right quadrant is labelled “Quadrant 4” and includes the positive numbers on the x-axis and the negative numbers on the y-axis.
We will be exploring the first quadrant of the Cartesian plane, where the numbers along the x- and y-axis are positive.
The first quadrant of a Cartesian plane. It has a vertical y-axis and a horizontal x-axis. Numbers on each axis are positive (greater than zero).
Coordinates
Coordinates are pairs of numbers which are used to describe the exact location of any point on the plane.
They refer to the intersection of two lines on a grid and are written inside a set of brackets.
The first number in the pair describes the horizontal value (x-axis), and the second number describes the vertical value (y-axis).
For example, consider the first quadrant of a Cartesian plane, which has values from 0 to 8 along the x-axis and 0 to 8 along the y-axis. The point of origin is (0,0).
There is a dot placed at the intersection of two lines on the grid.
To identify the location of the point we need to determine the distance of the point from the origin along the x- and y-axis.
Consider the following steps:
1. First, use the horizontal x-axis and count from the origin until you arrive at the grid line where the point is located. This dot is located at 4 along the x-axis.
A dot on the first quadrant of a Cartesian plane. Arrows show that the dot is 4 spaces to the right of the point of origin, located at 4 on the x-axis.
2. Then, use the vertical y-axis until you locate the dot. The dot is located at 3 on the y-axis.
For this dot, the coordinates identified are (4,3).
A dot on the first quadrant of a Cartesian plane. Arrows show that the dot is 4 spaces to the right of the point of origin, located at 4 on the x-axis. Another set of arrows show that the dot is located 3 spaces up from the point of origin, located at 3 on the y-axis. For this dot, the coordinate is (4,3).
Student Tips
Which axis?
It is important that you identify the x-axis number first, then the y-axis number.
They are separated by a comma and inside a set of brackets.
Your turn!
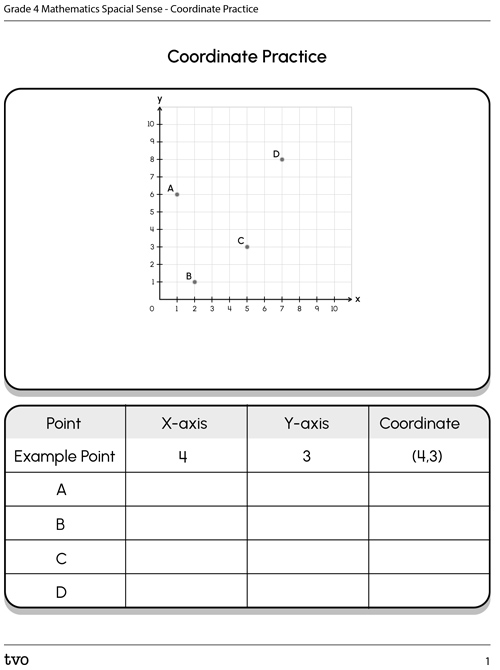
Explore the following Cartesian plane.
Determine the coordinates of the four points labelled on the plane.
You can record your ideas in the following fillable and printable Coordinate Practice document.You can also use another method of your choice.
When you are ready, press ‘Answers’ button to reveal the coordinates for the practice activity.
| Point | X-axis | Y-axis | Coordinate |
|---|---|---|---|
| Example Point | 4 | 3 | (4,3) |
| A | 1 | 6 | (1,6) |
| B | 2 | 1 | (2,1) |
| C | 5 | 3 | (5,3) |
| D | 7 | 8 | (7,8) |
Plotting points and changing location
Let’s practise plotting points on a Cartesian plane.
When plotting points, the first number in the coordinate describes where the point is located along the x-axis. The second number describes where the point is along the y-axis.
Task 1: Plot the points
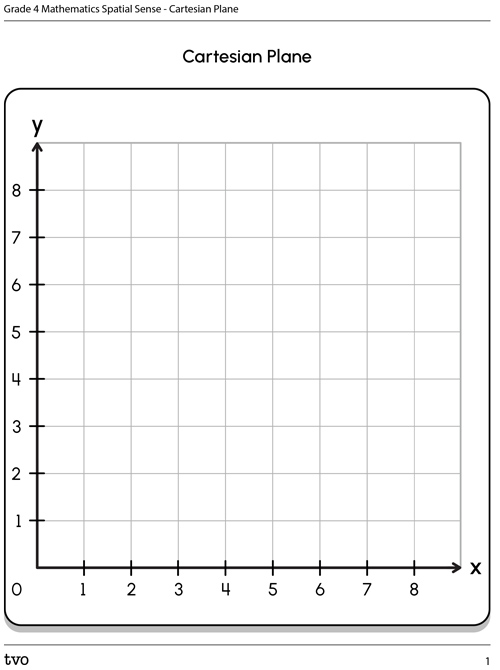
Explore the following points and plot them on a Cartesian plane.
| Point | Coordinates |
|---|---|
| Point E | (3,5) |
| Point F | (1,2) |
| Point G | (7,6) |
| Point H | (5,6) |
You can use the following fillable and printable Cartesian Plane document to plot the points. If you’d prefer, you can plot the points on grid paper, a digital grid, or use another method of your choice.
Task 2: Move the point
Consider Point E (3,5).
What would happen if it moved to a different location on a grid?
What if Point E is now at (6,1) how can we describe its movement?
Student Tips
Prime time
When the location of a point changes within the same grid we label the points with the same letters, but add a prime symbol (A′, B′, C′, D′) for the points. They are now read as A prime, B prime, C prime, and D prime
The following Cartesian plane has an x- and y-axis which ranges from 0 to 8. The point of origin is (0,0).
Two points are labelled on the plane: Point E (3,5) and Point E′ (E prime) (6,1)
Two dots, or points, on the first quadrant of a Cartesian plane. The x- and y-axes are each numbered from 0 to 8. Point E is plotted at coordinate (3,5). Point E prime is plotted at coordinate (6,1). Arrows on the grid indicate that Point E Prime moved 3 spaces to the right, and 3 spaces down.
To move this point, we start at Point E (3,5) and count 3 units right and 4 units down to get to the new coordinate of Point E′ (6,1).
We describe the horizontal distance first then the vertical distance.
Task 3: One more move
Consider the following Cartesian plane.
Two dots, or points, on the first quadrant of a Cartesian plane. The x- and y-axes are each numbered from 0 to 8. Point G is plotted at coordinate (7,6). Point G prime is plotted at coordinate (5,3).
On this Cartesian plane, Point G (7,6) moved to Point G′ (5,3). Describe how the point moved from G (7,6) to G′ (5,3) in a notebook or a method of your choice.
Student Tips
Describing movement
Describe the movement of the point using words like up, down, left, right and the number of units it moved.
Consolidation
Phases of the moon
One night the moon appears. Its two vertices are labelled A and B.
Nine days later, another phase of the moon has now appeared in the sky. The new moon is labeled with points A′ (A Prime) and B′ (B Prime).
The two moons and their vertices are plotted on the following Cartesian plane.
Two crescent moon shapes drawn on the first quadrant of a Cartesian plane. The x- and y-axes are each numbered from 0 to 8. The first crescent moon has a vertex labelled A at the coordinate (3,8), and another vertex labelled B at the coordinate (3,5). The second crescent moon has a vertex labelled A prime at the coordinate (6,7), and another vertex labelled B prime at the coordinate (6,4).
Press ‘Hint’ to reveal a helpful tip.
Identify the coordinates for A, B, A′ (A Prime), and B′ (B Prime). Then, describe how far the moon has moved.
Record your ideas in a notebook or a method of your choice.
Reflection
As you read through these descriptions, which sentence best describes how you are feeling about your understanding of this learning activity? Press the button that is beside this sentence.
I feel...
Now, record your ideas using a voice recorder, speech-to-text, or writing tool.