Minds On
Triangles on a Cartesian plane
Explore the following grids with triangles on them. What is happening on each grid? How does the triangle’s position change?
Record your ideas in a notebook or a method of your choice.
Action
What is a transformation?
Each image in the Minds On section represents a transformation of a triangle.

A transformation on a shape results in a change to the shape’s position or its size. The transformation describes the movement applied to a shape.
Transformations include:
- translations, which are slides
- rotations, which are turns
- reflections, which are flips
Task 1: Translations of a triangle
Translations move a shape without rotating, reflecting, or changing the size.
Imagine you place a sign on the floor and move it somewhere else in the room. As long as the sign is not rotated (or flipped), this would be a translation. We use directional words like right or left and up or down to describe the direction a shape is moved.

Let’s explore this video to learn how to translate a shape.
Translations, Copyright © 2021 The Ontario Educational Communications Authority. All rights reserved.
Practice
Translate the following triangle 3 units to the left and 2 units down. Record your answer using a method of your choice.

When you are done translating the triangle on your own, press ‘Answer’ to access the solution.
There is an 8 by 8 Cartesian plane. Triangle ABC has point A at (4,3), B at (5,7) and C at (7,4). The second triangle A prime, B prime, C prime is a translation of triangle ABC. It is 3 units to the left and 2 units down. The points on this second triangle are A prime (1,1), B prime (2,5), C prime (4,2).
Task 2: Reflections of a shape
Reflections flip a shape. An example of a reflection is to flip a sign to show the back of the sign.

Let’s explore this video to learn how to reflect a shape.
Reflections, Copyright © 2021 The Ontario Educational Communications Authority. All rights reserved.
Practice
Reflect the rectangle over the dotted line which is located at y = 3. Record your solution using a method of your choice.

When you are done reflecting the rectangle on your own, press ‘Answer’ to access the solution.
2 rectangles that are reflections of one another. The original rectangle, ABCD has points A at (3,6), B at (6,6), C at (3,4), D at (6,4). The reflected triangle, A prime, B prime, C prime, D prime has points A prime at (3,0), B prime at (6,0), C prime at (3,2), D prime at (6,2).
How else could you reflect the rectangle?
Task 3: Rotations of a Shape
A rotation is when you turn a shape around. Let’s explore a video to learn how to rotate a shape.
Rotations, Copyright © 2021 The Ontario Educational Communications Authority. All rights reserved.
Steps to rotating a rectangle
Consider the following steps when rotating a rectangle.
In order to rotate a rectangle, you need:
- a centre of rotation either on the shape itself or off the shape
- the angle
- the direction (clockwise or counterclockwise) at which the shape rotates
If using a protractor to rotate the rectangle:
- Place the centre of the protractor on the centre of rotation.
- Determine the angle of rotation and where the new points will be (for example, if we were rotating 90° counter-clockwise, we would identify where the 90° mark is).
- Examine the distance of the points from the centre of rotation when the 0° line intersects the points and count the number of spaces.
- Place the points at their new location, using the angle of rotation and the distance from the centre of rotation, and then connect the points of your shape.
Practice
Triangles are great shapes to play with if we want to rotate or reflect them. Let’s practice.
Use a pattern block triangle, one made of paper, or an interactive triangle. Decide on a point of rotation. Which point will stay still while the rest of the shape rotates?
Now rotate the triangle. You should notice that the point that is held in place does not move, but the other points will move places.

Now let’s try it on a Cartesian plane. When rotating any shape, you can use a protractor to get the angle correct. Also, the distance to the centre of rotation is the same for the original point as well as the rotated point.
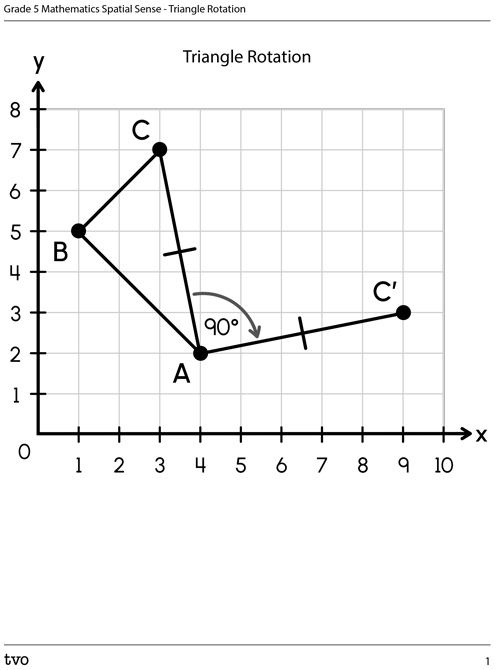
The following triangle is being rotated 90° clockwise with point A as the centre of rotation.
Point C has already been rotated. Using the same rotation, try plotting the image of point B.
Record your answer using a method of your choice.

Triangle on an 8 by 8 Cartesian plane with Point A at (4,2), B at (1,5), C at (3,7). Side AC of the triangle has been reflected 90 degrees. Point C prime is at (9,3), A prime is the same as A at (4,2).
You may use the following grid. Press the ‘Activity’ button to access the Triangle Rotation activity.
When you are done rotating the triangle, press ‘Answer’ to check if you rotated the triangle correctly.
8 by 8 Cartesian Plane. There are 2 triangles. Triangle A B C has Point A at (4,2), B at (1,5), C at (3,7). Triangle A B C prime has point A prime at (4,2), B prime at (7,5), C prime at (9,3).
Now, let’s try rotating a whole triangle.
Use the following graph or record your answers using a method of your choice.
- Identify each coordinate of triangle ABC.
- Rotate ABC 90° clockwise using point C as the centre of rotation.
- Identify each coordinate of the reflected triangle A′B′C′.

When you are done rotating the triangle on your own. Press ‘Answer’ to access a solution and check your answer.
Triangle A B C on a cartesian plan. Point A at (0,2), point B (2,8) and point C (4,3). The rotated triangle has points A prime at (3,7), B prime at (9,5) and C prime at (4,3).
Consolidation
Task 1: Reflecting a shape
Consider an empty Cartesian plane. (0,0) is at the origin where the x and y-axes intersect, and both the x and y-axes are numbered 0 to 8.
Place a shape on the plane. You can use pattern blocks, draw on paper, or use online manipulatives. Using what you have learned about coordinates, describe the location of the shape.
Reflect the shape on a horizontal reflection line AND a vertical reflection line. You can place the reflection lines anywhere you like.
Record your ideas in a notebook or a method of your choice.
Task 2: Translating a shape
Consider an empty Cartesian plane. (0,0) is at the origin where the x and y-axes intersect, and both the x and y-axes are numbered 1 to 8. Place a shape on the plane.
You can use pattern blocks, draw on paper, use online manipulatives, or create an audio recording.
Using what you have learned about coordinates, describe the location of the shape. Translate the shape 3 up and 4 across (left or right, your choice).
Now describe the new coordinates of the shape.
Record your thoughts on paper, on the computer, using speech-to-text, in an audio recording, or using a method of your choice.
Task 3: Transforming shapes
Now let’s practice transforming three different shapes and describing them in our own words.
Using the following grid, reflect this triangle over the line provided. Record this reflection in a notebook or a method of your choice.
A Cartesian plane has a triangle with vertices (2,5), (3,7) and (4,5). A line is drawn horizontal through 4 on the y-axis.
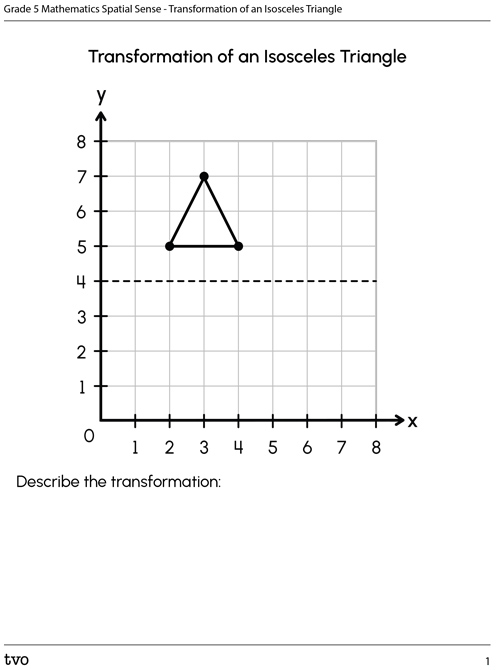
Press the Activity button to access the Transformation of an Isosceles Triangle.
Activity (Open PDF in a new tab)On the following grid, consider how much the bottom left triangle is moved to get the one in the top right? Be specific, for example, how many blocks (right or left and up or down) has it been moved? Record your response using a method of your choice.

Press the Activity button to access the Transformation of a Right Angle Triangle task.
Activity (Open PDF in a new tab)On the following grid, rotate the square 90° counterclockwise (the opposite direction a clock spins). Record the rotation in a notebook or a method of your choice.

Press the Activity button to access the Transformation of a Square task.
Activity (Open PDF in a new tab)Reflection
As you read through these descriptions, which sentence best describes how you are feeling about your understanding of this learning activity? Press the button that is beside this sentence.
I feel...
Now, record your ideas using a voice recorder, speech-to-text, or writing tool.
Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new tab)