Minds On
Mystery bags
Guess what flat, two-dimensional shapes are inside these mystery bags using the following information.
Record your ideas in a notebook or a method of your choice.

Mystery bag #1
There is a bag full of shapes. All together, the shapes have 9 sides. What shapes could be in the bag?
Come up with as many different answers as you can. Are they the same shapes or different?
Mystery bag #2
There is another bag full of shapes. All together, they have 36 vertices. What shapes could be in the bag?
Come up with as many different answers as you can. Are they the same shapes or different?
Brainstorm
Brainstorm
Would knowing the number of shapes in the bag affect your answers for each bag? How?
Record your ideas in a notebook or a method of your choice.

Action
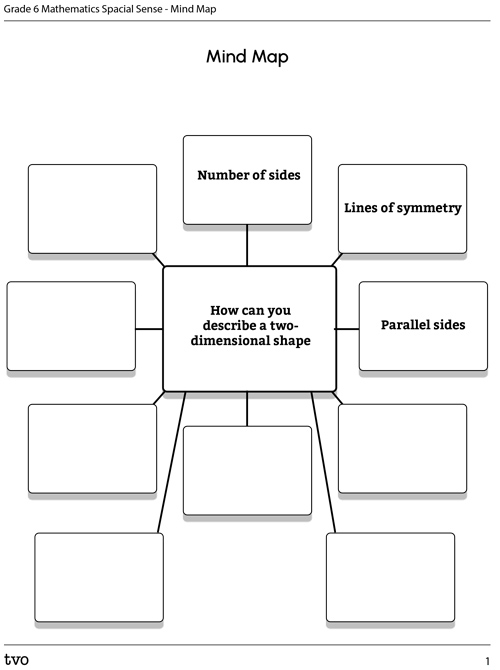
Task 1: Properties of two-dimensional shapes
A property, or an attribute, of a shape is a feature of the shape that it describes. Some examples include number of sides, parallel sides, or lines of symmetry.
Create a list of all the attributes that could be used to explain a two-dimensional shape. Use a mind map or another organization method of your choice to record your ideas.
Complete the Mind Map in your notebook or using the following fillable and printable document.
You can also use another method of your choice.
Task 2: List the properties
Two-dimensional shapes are all around us. Explore the following examples of two-dimensional shapes.
Choose which of the attributes listed can be used to explain each of the shapes in the pictures.
- It has all equal angles.
- It has 2 sets of parallel lines.
- It has perpendicular angles.
- It has 8 sides.
- All angles are acute.
- It has obtuse angles.
- It has more than 2 sets of parallel lines.
- It has more than 1 line of symmetry.
Record your ideas in a notebook or a method of your choice.
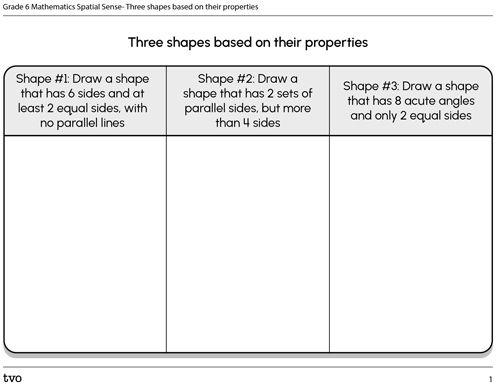
Task 3: Create shapes based on their properties
Use a digital drawing program, pen and paper, or popsicle sticks/toothpicks to create the following. Complete the Shapes and Properties Chart in your notebook or using the following fillable and printable document.
Press the Activity button to access the Shapes and Properties Chart.
Activity (Open PDF in a new tab)You can also use a method of your choice to describe the shape you would create with the following constraints.
Shape #1: A shape that has 6 sides and at least 2 equal sides, with no parallel lines
Shape #2: A shape that has 2 sets of parallel sides, but more than 4 sides
Shape #3: A shape that has 8 acute angles and only 2 equal sides
Task 4: Using properties to name quadrilaterals
The properties of a shape help to determine whether a shape can fit into a category or be labeled in a certain way. We use properties to describe different types of quadrilaterals. A quadrilateral is any shape that has 4 sides.
Explore the properties.
Properties of two-dimensional shapes. List property in one colour, then definition, then drawing example as follows… Parallel sides: number of pairs of parallel sides, if the opposite sides continue, they will never intersect. Side lengths: number of pairs of equal side lengths. Vertices: number of vertices, the points where 2 sides meet. Sides: number of lines or side lengths. Lines of symmetry: number of lines of symmetry, lines that can be drawn through the shape where both sides of the line are exactly the same. Angles: number of angles (where 2 lines meet) or type of angles (acute, obtuse, or right). Diagonals: where 2 lines intersect when they are drawn diagonally from corner to corner of the shape.
Choose an example of a quadrilateral.
Press ‘Hint’ to access some examples of quadrilaterals.
You will create the same quadrilateral three times. Each time, change the side lengths, angles, orientation, etc. You can draw or construct them using a digital program, pen and paper, sticks, plasticine, string, or use a method of your choice to describe the shape you would create.
Answer the following questions about the properties of your quadrilaterals. If all of your shapes have the same things in common, that attribute can be used to define or describe the shape.
- Angles: How many right angles are there? How many reflex angles (greater than 180°) are there?
- Equal sides: How many equal sides are there? Are the equal sides opposite or adjacent?
- Parallel sides: How many sets of parallel sides are there?
- Symmetry: Are there any lines of symmetry?
- Diagonals: When you add 2 diagonal lines through the shape, do they intersect in the middle of the shape? Are they equal in length?
Summarize your answers. How might you describe or define your given shape?
Record your ideas in a notebook or a method of your choice.
Task 5: Relationship of quadrilaterals
What do you think the following graphic means?
Venn diagram showing the subsets of Quadrilaterals. Quadrilaterals is in the outermost circle. The first subset is Trapezoid. Within Trapezoid is the subset Parallelogram. Parallelogram contains three subsets: Rectangle, Square and Rhombus. Each of these are in their own subset. Another subset of quadrilaterals includes Square, Rhombus and Kite. Kite does not belong to any of the other subsets.
When you are ready, press ‘Answer’ to access an explanation.
Now, consider the following questions:
- What makes a square special?
- What is the relationship between a square and a rhombus, rectangle, kite, parallelogram, or trapezoid?
Record your ideas in a notebook or a method of your choice.
Task 6: Sorting shapes
We can use any of the properties listed earlier to sort a group of shapes. One way that we can do this is using a Venn diagram.
Explore the following Venn diagram example.
One side of the Venn diagram says “At least 2 sets of equal sides,” and the other side says, “No right angles.” A square and a rectangle have 2 sets of equal sides, a circle and isosceles trapezoid have no right angles, and a hexagon and octagon have both. A scalene right triangle does not fit any of these categories.
Now, it’s your turn! Choose two attributes and sort a variety of shapes into your Venn diagram, or describe how you would sort a variety of shapes using two attributes. If the shape has neither attribute, you can leave it outside of the Venn diagram.
If you would like, you can complete the activity using TVO Mathify. You can also use your notebook or the following fillable and printable document.
Press the ‘TVO Mathify’ button to access this resource and the ‘Activity’ button for your note-taking document.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Task 7: Guess the sorting rule
Explore the following Venn diagram. Determine the sorting rule, and then sort the remaining shapes accordingly. Come up with as many possibilities as you can.
The left circle of the Venn diagram is labelled “Attribute 1.” This section contains a parallelogram. The right circle of the Venn diagram is labelled “Attribute 2.” This section contains a triangle. In the section where the two circles overlap, there is a square. Below the diagram, there is a rectangle, a trapezoid, a rhombus, a hexagon and a rhombus.
If you would like, you can complete the Venn Diagram with Shapes using TVO Mathify. You can also use your notebook or the following fillable and printable document.
Press the ‘TVOMathify’ button to access this resource and the ‘Activity’ button for your note-taking document.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Consolidation
Task 1: Riddles

Determine which shape each of the following riddle is describing. Justify your answer using the properties of two-dimensional shapes. Record your ideas using a method of your choice.
- I have more than 1 right angle and 2 sets of parallel lines. My opposite sides are the same length. What am I?
- I have 2 obtuse angles and 2 acute angles. One set of opposite sides is equal in length. What am I?
- I have no parallel lines, but 1 line of symmetry. I am not a quadrilateral. What am I?
Task 2: Create your own riddles
Create three riddles of your own. Consider the following when creating your riddles:
- choose a two-dimensional shape
- use its properties to create a description
- give enough information, but not too much!
Record the riddles using a method of your choice.
Reflection questions
Reflect on and answer the following questions:
- Why is it important to identify properties of shapes? When would you want to sort shapes?
- What skills can help you identify properties of shapes?
- What strategies did you use to find the answer to shape riddles?
Record your ideas in a notebook or a method of your choice.
Reflection
As you read through these descriptions, which sentence best describes how you are feeling about your understanding of this learning activity? Press the button that is beside this sentence.
I feel...
Now, record your ideas using a voice recorder, speech-to-text, or writing tool.
Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window)