Learning about radius, diameter, and circumference

Consider the image provided.

What would happen if you were to fold the circle in half?

What if you were to fold it in half again, perpendicular to the first fold (or line)? How could you identify the centre of the circle?

Press ‘Answer’ to see the solution.

Answer

Complete Radius and Diameter in your notebook or using the following fillable and printable document.

The tasks is as follows:

• Using a ruler, draw and measure a line from the centre of the circle to any point on the outside edge. This is a radius.

Repeat this action a couple of times. You will notice that the distance is always the same between the centre point and outside edge.

• Draw a line from one side of the circle to the other making sure it passes through the centre. This is the diameter.

Measure the diameter of the circle.

• What do you notice about the relationship between the diameter and the radius?

The diameter is 2 times the radius. The relationship can by represented as 2r = d or r = ½ d.

• Draw and measure any two lines from one side of the circle to the other. Compare these measurements with the measurement of the diameter above. What is the relationship between these measurements?

The diameter of a circle is the longest distance from one side of a circle to another. It must pass through the centre of the circle.

Record these “circle” properties and relationships.

Press ‘Circle Properties’ to check your answers about circle properties and relationships.

Circle Properties

Measuring circles

Press the following tabs to review what we have learned so far.

Task 1: Investigating mathematical relationships

It’s time to investigate some circles.

You will need a couple of circles and/or cylinders (e.g., a drinking glass, cooking pot, can, or clock).

You will also need a ruler, and string, or something like a string (e.g., a piece of yarn, dental floss, shoelace, or ribbon).

1. Wrap string or ribbon around a circle (or cylinder). Then, line it up against the ruler to determine the circumference.

Circumference is the distance around a circle, or its perimeter.

Take for example, a round clock.

When a piece of string was put around the outside of the clock, and then lined up against the ruler, it was 97 cm. The circumference, or its perimeter, is 97 cm.

2. For each object measure:

• the diameter to the nearest 0.1 cm
• the circumference to the nearest 0.1 cm

For example, the diameter of the clock was measured using a piece of string, going from one edge of the clock to the other, crossing through the centre, and it was 30.5 cm.

3. For each object, calculate the circumference divided by the diameter.

• What do you notice about the results of your calculations?

Describe the relationship between the diameter and the circumference.

Press ‘Answer’ to reveal the learning concept.

Answer

Task 2: Determining task 1

In mathematical language, pi (π) is the mathematical symbol used to describe the quotient of the circumference of any circle divided by its diameter, often represented as 3.14.

π isn’t exactly 3.14; that’s an approximation. π is called an irrational number because the numbers after the decimal keep going, but don’t repeat in a pattern. To 11 decimal places π is 3.14159265359…

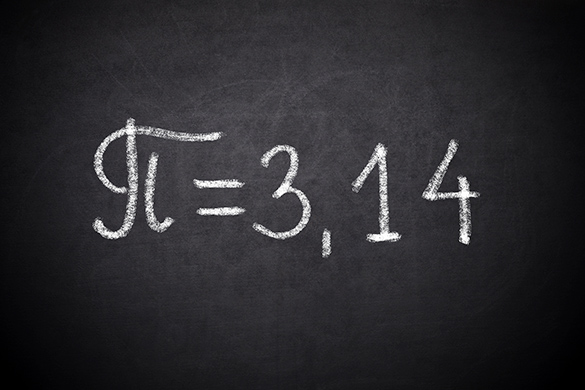
We commonly use 3.14 in calculations. All scientific calculators have a π button, if you need more accuracy for a calculation.

Formula for Circumference using diameter:

• Circumference = diameter × π
• Circumference = π × diameter
• C = πd

For each circle in the table, use the radius to determine the diameter.

Then, use the diameter and the value π = 3.14 to determine the circumference of the circle.

Complete Diameter and Circumference in your notebook or using the following fillable and printable document.

Press ‘Solution’ to access Diameter and Circumference Answers.

Task 3: Practice with circumference

In Tasks 1 and 2, you investigated the relationship between the diameter, $\pi$, and circumference.

The formula for calculating circumference is:

C = πd

Let's practise using the formula for circumference. Use 3.14 as the value for $\pi$.

The following is a matching activity. Match the diameter of a circle with the circumference of that circle.

Building a community garden

The Eco Club at a school decided to plant a community garden for students to learn more about caring for plants. The round garden plot has a diameter of 4.65 m.

Calculate the circumference of the garden.

The students then decided to build a simple fence around the garden bed to protect it from people walking over the newly sprouting plants. The fence is placed 44 cm away from the outer edge of the garden.

Calculate the circumference of the fence.

TIP: Pay careful attention to units.

Record your thinking using a method of your choice.

Consolidate your learning

Reflect on your learning by describing the relationship between the radius, the diameter, and the circumference of a circle. Provide 1-2 examples. Record your thinking using a method of your choice.

Reflection

As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.

Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.

When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.

Connect with a TVO Mathify tutor