Minds On
Tessellation
Reflections, rotations, and translations produce congruent shapes.
When congruent shapes are transformed and duplicated in such a way that they completely cover a surface without any gaps or overlaps, this is called a tessellation.
Consider the following ‘L’ shapes. Can you think of a way to duplicate and tessellate them so that they completely cover the grid?

A ten-by-ten grid with two congruent ‘L’ shapes. Both ‘L’ shapes consist of four squares. They are two squares wide and three squares tall. The second shape has been rotated one-hundred-and-eighty degrees (or reflected horizontally and vertically) and translated two squares right from the first shape.
If you would like, you can complete this activity using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.

Press the ‘TVOMathify’ button to access this resource and the ‘Activity’ button for your note-taking document.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Once you have completed your tessellation, press ‘Suggested Answer’ to reveal one possible solution.

A ten-by-ten grid with two congruent ‘L’ shapes tessellated to completely cover the grid. Both ‘L’ shapes consist of four squares. They are two squares wide and three squares tall. The second shape has been rotated one-hundred-and-eighty degrees (or reflected horizontally and vertically) and translated one square right and one square down from the first shape, creating a composite of both ‘L’ shapes. This composite shape is duplicated and translated in four ways: translating one square right, and two squares up; translating one square left, and two squares down; translating three squares right, and two squares down; and translating three squares left, and two squares up. These duplications and translations of the composite shape are repeated so that the grid is completely covered without any gaps or overlaps.
Tiles

The shape or combination of shapes that are duplicated and transformed to create a tessellation are called tiles.
Tessellated tiles are always symmetrical. For example, the two congruent ‘L’ shapes from our activity combine to form a symmetrical tile that is duplicated and translated to tessellate the grid.
Action
Tessellating shapes
A tessellation is a pattern made up of one or more shapes that completely covers a surface without any gaps or overlaps. You may have seen a tessellation before in the patterns made by floor tiles. If you can tile the floor using a shape without having any gaps or overlaps, then this shape can tessellate.

Which shapes tessellate?
Do you know any shapes that tessellate?
Let’s explore ten common shapes to find out which tessellate, and which do not.
If you would like, you can complete this activity using TVO Mathify. You can also use your notebook or the following fillable and printable document.
Press the ‘TVO Mathify' button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Once you have completed your tessellation, press ‘Suggested Answer’ to reveal one possible solution.
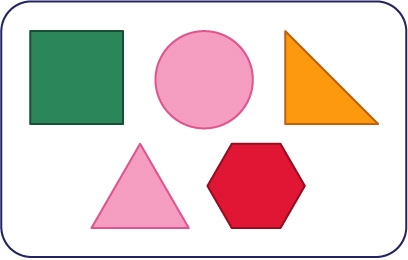
Shapes that tessellate

A hexagon can tessellate by translating congruent hexagons so that they are arranged edge-to-edge, with three hexagons meeting at each vertex. A square can tessellate by translating congruent squares so that they are arranged edge-to-edge, with four squares meeting at each vertex. An equilateral triangle can tessellate by translating congruent triangles into rows, then rotating every other triangle one-hundred-and-eighty degrees (or horizontally reflecting every other triangle) so that they are arranged edge-to-edge, with six triangles meeting at each vertex. A right-angle triangle can tessellate by translating congruent triangles into rows, then rotating every other triangle one-hundred-and-eighty degrees (or horizontally reflecting every other triangle) so that they are arranged edge-to-edge, with six triangles meeting at each vertex. A rhombus can tessellate by translating congruent rhombuses into rows, then rotating every other rhombus one-hundred-and-eighty degrees (or horizontally reflecting every other rhombus) so that they are arranged edge-to-edge, with four rhombuses meeting at each vertex. A rectangle can tessellate by translating congruent rectangles so that they are arranged edge-to-edge, with four rectangles meeting at each vertex. A parallelogram can tessellate by translating congruent parallelograms so that they are arranged edge-to-edge, with four parallelograms meeting at each vertex.
Shapes that don't tessellate

A circle does not tessellate. Congruent circles have been translated so that they are arranged side-by-side, and a concave diamond-shaped gap is left between the circles. A pentagon does not tessellate. Congruent pentagons have been translated and rotated so that they are arranged edge-to-edge, and an isosceles triangle-shaped gap is left between the pentagons. An octagon does not tessellate. Congruent octagons have been translated so that they are arranged edge-to-edge, and a square-shaped gap is left between the octagons. Congruent octagons have also been translated and rotated, and chevron and triangle-shaped gaps are left between the octagons.
Tessellation transformations
Consider the seven common shapes that tessellate. What transformations did you use to tessellate these shapes?
All shapes use translations to tessellate. Some shapes also use rotations and reflections to tessellate. In the suggested answers from our previous activity, notice that some triangles and rhombuses are upside down compared to others. These reflections show that the shapes are symmetrical.
Review the ‘L’ shapes from our Minds On activity. What transformation describes their two different orientations?

A six-by-five grid with two congruent ‘L’ shapes. Both ‘L’ shapes consist of four squares. They are two squares wide, and three squares tall. The second shape has been rotated one-hundred-and-eighty degrees (or reflected horizontally and vertically) and translated two squares right from the first shape.
Press ‘Suggested Answer’ to reveal possible solutions.
- A rotation of 180°
OR
- A horizontal reflection and a vertical reflection
Geometric properties of tessellating shapes
Tessellating shapes can fit together in a repeating pattern with no gaps or overlaps.
Do you notice anything special about the shapes that tessellate compared to the shapes that do not?
The common geometric property of shapes that tessellate is that the sum of their interior angles at the vertex where the shapes meet equals 360°.

A tessellated square has four interior angles of ninety degrees at every vertex, equalling three-hundred-and-sixty degrees. A tessellated equilateral triangle has six interior angles of sixty degrees at every vertex, equalling three-hundred-and-sixty degrees. A tessellated hexagon has three interior angles of one-hundred-and-twenty degrees at every vertex, equalling three-hundred-and-sixty degrees.
With shapes that do not tessellate, the sum of their interior angles at the vertex where the shapes meet does not equal 360°. This results in gaps or overlaps between the shapes.
For example, a tessellated pentagon will have gaps between shapes, and a tessellated heptagon with have overlaps between shapes.

A tessellated pentagon has three interior angles of one-hundred-and-eight degrees at every vertex, equalling three-hundred-and-twenty-four degrees. This leaves an isosceles-shaped gap between pentagons. A tessellated heptagon has three interior angles of one-hundred-and-twenty-eight-point-five-seven degrees at every vertex, equalling three-hundred-and-eighty-five-point-seven-one degrees. This leaves a kite-shaped overlap between heptagons.
Some shapes do not tessellate on their own, but do tessellate with the addition of other shapes.
For example, a tessellated octagon will have square gaps between shapes, so an octagon and a square with the same side lengths will tessellate. We know an octagon and square can tessellate together because the sum of their interior angles at the vertex where the shapes meet equals 360°.

An octagon tessellated with a square of equal sides has two interior angles of one-hundred-and-thirty-five degrees, and one interior angle of ninety degrees at every vertex, equalling three-hundred-and-sixty degrees.
The tiles formed by combining octagons and squares are symmetrical because they can be reflected, rotated, or translated and still appear the same.
Some shapes can be symmetrical, but not have the geometric properties to tessellate. For example, a circle is symmetrical, but does not have corners, so a tessellated circle will have gaps between shapes because there are no interior angles to form vertices.

Determining tessellating transformations
Up to this point, we’ve mostly considered regular polygons, which are shapes with sides that are all the same length.
Do irregular polygons still tessellate? Consider the following irregular polygon, an arrow shape:

When we have a symmetric shape, we need to determine which transformations to apply to create a tessellation.
What transformations were applied to the following tessellation of the arrow shape?

Three right-facing arrows are positioned so the tip of one arrow touches the end of another arrow. This pattern is repeated in three rows where the sides of each arrow touch. The spaces left between the arrows are in the shape of four left-facing arrows.
How would you describe the transformations that relate the left and right facing arrows in the tessellation?
Press ‘Suggested Answer’ to reveal possible solutions.
- A rotation of 180°
OR
- A horizontal reflection and a vertical reflection
Tessellating irregular polygons
We are now going to practice transforming irregular polygons to create tessellations.
If you would like, you can complete this activity using TVO Mathify. You can also use your notebook or the following fillable and printable document.
Press the ‘TVO Mathify' button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Once you have finished tessellating the irregular polygons, press ‘Suggested Answers’ to reveal possible solutions.

A scalene triangle can tessellate by translating congruent triangles into rows, then rotating every other triangle one-hundred-and-eighty degrees (or horizontally reflecting every other triangle), so that they are arranged edge-to-edge, with six triangles meeting at each vertex. A quadrilateral can tessellate by translating congruent quadrilaterals into rows, then rotating every other quadrilateral one-hundred-and-eighty degrees (or horizontally reflecting every other rhombus) so that they are arranged edge-to-edge, with four quadrilaterals meeting at each vertex. A chevron can tessellate by translating congruent chevrons, so that they are arranged edge-to-edge, with three chevrons meeting at each vertex.
- What transformations did you need to apply to each irregular polygon to create a tessellation?
Record your answers using a method of your choice.
Consolidation
Tile design
Someone is designing their new home and they need a unique design for the tiles on the floor. They want a change from simple squares and rectangles.
Can you think of a unique shape that will tessellate?
Using a method of your choice, create a tile design, and record a description of the transformations that you apply to create your tessellation.
If you need ideas, explore the following carousel of tessellations:
Reflection
As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.
I feel...
Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.
When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.
Press ‘Discover More’ to extend your skills.
Discover MoreThink about careers that might require extensive knowledge of tessellations.
Research to explore how many of these careers you can find.
- Which career interests you the most? Why?
Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window)

