Minds On
Formulas

Select the correct answer, and then press ‘Check Answer’ to see how you did.
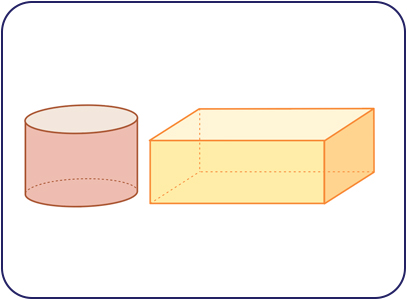
For each three-dimensional shape, select the corresponding volume formula.
Press ‘Let’s check!’ to reveal the formulas for area and volume.
| Shapes | Area formulas |
|---|---|
| Rectangle | |
| Triangle | |
| Parallelogram | |
| Trapezoid | |
| Circle |
| Three-dimensional shapes | Volume formulas |
|---|---|
| Prism | |
| Cylinder |
Action
Composite objects
Composite objects are three-dimensional objects that are made up of other objects, and when shapes are added together.
For instance, most buildings are composite objects.
Check out another example:

Select the correct answer, and then press ‘Check Answer’ to see how you did.
Press ‘Let’s check!’ to reveal the composite objects for a house.
A house can be separated into two three-dimensional objects:
- a triangular prism
- a rectangular prism
Brainstorm
Let’s think!
Take a moment to reflect on the following question:
How can we calculate the surface area and volume of a three-dimensional composite object?
Surface area of composite objects
Explore the following instructions to calculate the surface area of a three-dimensional composite object:
1. First, divide the object into three-dimensional objects.
2. Then, calculate the surface area of each object.
3. Lastly, add the surface areas for each object altogether to get the total surface area of the three-dimensional composite object.
Let’s calculate!

A house is divided into two composite objects, a triangular prism and a rectangular prism. The triangular prism has a width of 12 metres, and triangle height of 3 metres. The triangle itself is isosceles with 2 side lengths which are 5 metres, and the base of the triangle is 8 metres.
The rectangular prism has a length of 8 metres, width of 12 metres, and height of 6 metres.
Rectangular prism
Let’s calculate the surface area of the house together.
To calculate the surface area of the rectangular prism, calculate the area of each face.
Press on the faces of the prism and total surface area to reveal the surface area calculations of the rectangular prism in the composite object.
Since there are two faces (front and back), we will multiply by 2:
Since there are two sides, we will multiply by 2:
To calculate the total surface area, add up the totals for each part altogether.
To calculate the surface area of a triangular prism, calculate the surface area of its base, two sides, and two faces.
Note: In this situation, the bottom base of the triangular prism will not be calculated.
Student Tips
Did you know?
To calculate the surface area of each of the faces, we can calculate the area of the triangle:
Press on the faces of the prism and total surface area to reveal the surface area calculations of the triangular prism in the composite object.
Since there are two faces, we will multiply by 2:
To calculate surface area of the two side faces of the triangular prism, we need to know the measurement of the other sides of the triangular base.
Note: The side’s length measures 5 metres.
Since there are two sides, we will multiply by 2:
To calculate the total surface area, add up the totals for each part altogether.
Total surface area
Now that we have calculated the surface area of each composite object, we can add their surface areas altogether to get the total:
Therefore the total surface area of the composite object is
Note: In our total surface area calculations we ignored the top face of the rectangular prism and the bottom face of the triangular prism because it is on the inside of the shapes and not the surface.
You try!

Let’s explore the following composite object:
A composite object is constructed of two three-dimensional objects. The object on top has a radius of 2 metres, and a height of 4 metres. The object on the bottom has a length of 10 metres, a width of 5 metres, and a height of 3 metres.
The rectangular prism has a length of 10 metres, width of 5 metres, and height of 3 metres.
Select the correct answer, and then press ‘Check answer’ to see how you did.
If you would like, you can complete the this activity using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.
Press the ‘TVOMathify’ button to access this resource and the ‘Activity’ button for your note-taking document.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Press on the surface areas to reveal the calculations for the Cylinder and Rectangular Prism activity.
1. What is the formula for calculating the surface area of a cylinder?
area of base (circle) area of base (circle) circumference of the circle height of the cylinder.
2. What is the formula for calculating the surface area of a rectangular prism?
(2 area of the side face) (2 area of the front face) (2 area of the bottom face)
To calculate the total surface area, add up the totals for each part altogether.
Volume of three-dimensional composite objects

Explore the following instructions to calculate the volume of a three-dimensional composite object:
- First, divide the object into three-dimensional objects.
- Then, calculate the volume of each object.
- Lastly, add the volume for each object altogether to get the total volume of the three-dimensional composite object.
A house is divided into two composite objects, a triangular prism and a rectangular prism. The triangular prism has a width of 12 metres, and triangle height of 3 metres. The triangle itself is isosceles with 2 side lengths which are 5 metres, and the base of the triangle is 8 metres.
The rectangular prism has a length of 8 metres, width of 6 metres, and height of 12 metres.
For the following sentence, select the missing words.
Let’s calculate!
If you would like, you can complete the this activity using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.

Press the ‘TVOMathify’ button to access this resource and the ‘Activity’ button for your note-taking document.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Press ‘Let’s check!’ to reveal the calculations for the Volume of Composite Objects activity.
1. What is the formula for calculating the volume of a rectangular prism?
area of the base the height
2. What is the formula for calculating the volume of a triangular prism?
(base of the triangle) height of the triangle length of the prism
3. What is the total volume of the three-dimensional composite object?
Now that we have calculated the volume of each composite object, we can add their volumes altogether to get the total:
Therefore, the total volume area of the house is .
You try!
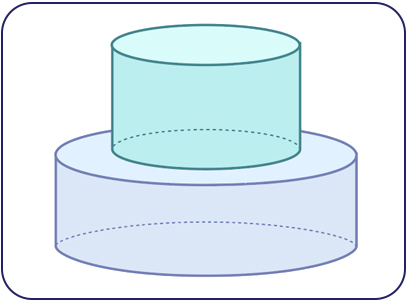
Examine the following cylinders:
There are two cylinders stacked on top of each other. The bottom cylinder is wider than the top cylinder. The bottom cylinder has a diameter of 9 centimetres and a height of 2 centimetres. The top cylinder has a radius of 3 centimetres and a height of 3 centimetres. The top cylinder is labelled Cylinder 1. The bottom cylinder is labelled Cylinder 2.
Consider:
- What two objects make up this three-dimensional composite object?
- What is the formula for calculating the volume of Cylinder 1?
- What is the volume of Cylinder 1? Cylinder 2?
- What is the total volume of this three-dimensional composite object?
If you would like, you can complete this activity using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.
Press the ‘TVOMathify’ button to access this resource and the ‘Activity’ button for your note-taking document.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Press the following tabs to reveal the calculations for the Volume of Stacked Cylinders activity.
1. What two objects make up this three-dimensional composite object?
There are two cylinders of different sizes that make up this three-dimensional composite object.
2. What is the formula for calculating the volume of a cylinder?
3a. What is the volume of Cylinder 1?
3b. What is the volume of Cylinder 2?
4. What is the total volume of this three-dimensional composite object?
Now that we have calculated the volume of each composite object, we can add their volumes altogether to get the total:
Therefore, the total volume of the composite object is
Brainstorm
What do you think?
You have calculated the surface area and volume of three-dimensional composite objects.
Do you notice anything about how they are related?
Consolidation
Create a composite object

- Create a three-dimensional composite object and describe how someone could calculate the surface area and volume.
- Include all of the steps and important details for them.
You may use sketches, concrete objects, or another method of your choice to help support your thinking!
Consider:
- What two objects did you use?
- What is the surface area of Object 1? Object 2?
- What is the volume of Object 1? Object 2?
- What is the total surface area? Total volume? Is there a relation? Explain.
If you would like, you can complete this activity using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.
Press the ‘TVO Mathify’ button to access this resource and the ‘Activity’ button for your note-taking document.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Reflection
As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.
I feel...
Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.
When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.
Press ‘Discover More’ to extend your skills.
Discover MoreCube with a cylindrical hole
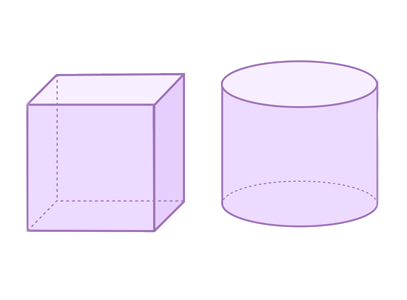
How could you calculate the surface area and volume of the following three-dimensional composite object?
Cube with side length of 10 centimetres. The cube has a cylindrical hole in the centre of the cube, from one end of the cube to the other. This hole has a diameter of 5 centimetres.
Note: There is a hole down the centre of the object.
There is a cube with side lengths of 10 cm. The cube has a hole going through it from end to end. This cylindrical hole has a diameter of 5 cm.
Consider:
- What two objects do you see in this diagram?
- What is the surface area of the cube?
- What is the surface area of the cylinder?
- What is the volume of the cube?
- What is the volume of the cylinder?
- What is the actual surface area of the three-dimensional object?
- What is the actual volume of the three-dimensional object?
If you would like, you can complete the next activity using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.
Press the ‘TVOMathify’ button to access this resource and the ‘Activity’ button for your note-taking document.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window)