Minds On
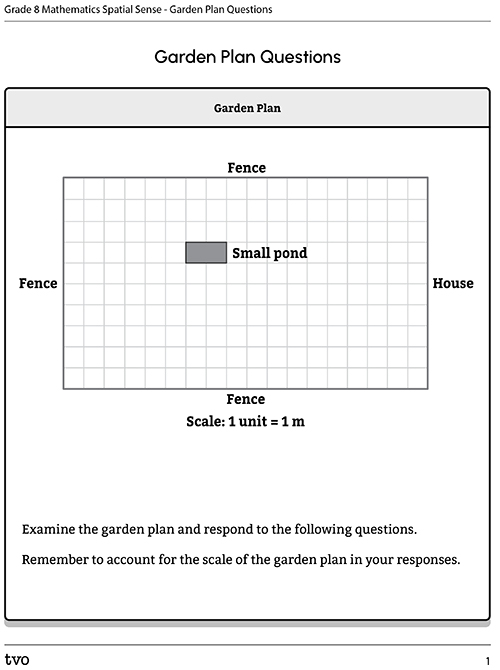
Garden designs
A landscaper has designed a new garden and needs to answer some questions about their plan.

Complete the Garden Plan Questions in your notebook or using the following fillable and printable document. You can also record your responses using a method of your choice.
Designing a garden
The gardener needs to design a garden for a new customer. Create a garden design by following the gardener’s instructions.

If you would like, you can complete this activity using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.
Press the ‘TVO Mathify' button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Action
Determining scale
Scale representations allow something very large or very small to be displayed on a page or on a screen. Scale representations are used for:
- visualizing, comparing, and calculating dimensions
- examining a map, following instructions, or designing a plan
In our Minds On activity, one unit on the garden plan was equal to one metre in reality. This can also be represented as a scale ratio.
Scale ratios
Examine the following Cartesian plane. If triangle is the original shape, what is the scale factor that it has been dilated by to create triangle

Two triangles are plotted on a Cartesian plane. The scale of the x-axis starts at zero and goes up by twos to ten. The scale of the y-axis starts at zero and goes up by twos to ten. Triangle P Q R has the coordinates P(1,3), Q(3,1) and R(1,1). Triangle P-prime Q-prime R-prime has the coordinates P-prime(3,9), Q-prime(9,3), and R-prime(3,3).
- Triangle has been dilated by a scale factor of three to form triangle
We know this because the lengths of each side of triangle are three times longer than the lengths of each side of triangle .
This can be represented as a scale ratio of 1∶3.
Ratio tables
We can use ratio tables to help us understand how the original size of an object in a scale representation has changed. We can then calculate the size of the dilated object.
Let's use a ratio table to calculate the size of an object that is dilated to be twice as big.
Complete the Rectangle Ratio Table in your notebook or using the following fillable and printable document. You can also record your answers using a method of your choice.
Press ‘Suggested Answer’ to reveal the solution.

Two rectangles on a 14 by 15 grid. The dilated rectangle has a base of ten units and a height of six units. The original rectangle has a base of five units and a height of six units.
| Original rectangle size | Dilated rectangle size | |
|---|---|---|
| Base | 5 units | 10 units |
| Height | 3 units | 6 units |
| Area (b × h) | 15 units2 | 60 units2 |
Now determine the missing measurements and scale ratios in the following ratio tables.
Complete Ratio Tables in your notebook or using the following fillable and printable document.
| Ratio Table One | ||
|---|---|---|
| Original rectangle size | Dialated rectangle size | |
| Base | 7 units | 1 unit |
| Height | 14 units | |
| Area (b×h) | 98 units2 | |
| Scale ratio | ||
| Ratio Table Two | ||
|---|---|---|
| Original rectangle size | Dialated rectangle size | |
| Base | 3 units | 9 unit |
| Height | 12 units | |
| Area (b×h) | 12 units2 | |
| Scale ratio | ||
Press the ‘Activity’ button to access the Ratio Tables.
Press ‘Suggested Answer’ to reveal the solutions.
| Ratio Table One | ||
|---|---|---|
| Original rectangle size | Dialated rectangle size | |
| Base | 7 units | 1 unit |
| Height | 14 units | 2 units |
| Area (b×h) | 98 units2 | 2 units2 |
| Scale ratio | 7∶1 | |
| Ratio Table Two | ||
|---|---|---|
| Original rectangle size | Dialated rectangle size | |
| Base | 3 units | 9 unit |
| Height | 4 units | 12 units |
| Area (b×h) | 12 units2 | 108 units2 |
| Scale ratio | 1∶3 | |
Creating scale representations
Review the following measurements of the front face of a school building:
| Base | 36 m |
|---|---|
| Height | 12 m |
| Features | Two windows with a base of three metres and a height of three metres. |

Create a scale representation of the front of the school building using the scale ratio of 300∶1 This means that one centimetre on your scale representation is equal to three metres (or three hundred centimetres) of the actual school building.
If you would like, you can complete this activity using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.
Press the ‘TVO Mathify' button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)If you need help determining the measurements for your scale representation, Press ‘Suggested Answer’ to reveal the solution.
| Original measurement | Scale ratio of 300∶1 | Scale drawing measurement |
|---|---|---|
| 36 m (or 3,600 cm) | 3,600 ÷ 300 = 12 | 12 cm (or 0.12 m) |
| 12 m (or 1,200 cm) | 1,200 ÷ 300 = 4 | 4 cm (or 0.04 m) |
| 3 m (or 300 cm) | 300 ÷ 300 = 1 | 1 cm (or 0.01 m) |
Consolidation
Creating a scale representation of a room
Scale representations are used to create floorplans, to build furniture, or to explore maps.
Review the following floorplan of a bedroom and its contents.

A floorplan of a bedroom and two closets is drawn with dimensions. The bedroom has a base of six metres, and a height of four metres, and contains a bed and a dresser. The bed has a base of two metres and a height of one metre. The dresser has a base of one metre and a height of two metres. Closet A is attached to the upper left corner of the bedroom, with a width of 2 metres and a height of 2 metres. Closet B is attached to the upper left side of the bedroom, with a width of 3 metres and a height of 2 metres.

Create a scale representation of the bedroom. Determine the scale ratio and record your calculations.
If you would like, you can complete this activity using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.
Press the ‘TVO Mathify' button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window) Activity (Open PDF in a new window)Reflection
As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.
I feel…
Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.
When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.
Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window)