Minds On
Base-10 place value
Let’s consider the number one.
What do you need to do to the number one so that it can be in the tens place instead of the ones place?
Press ‘Hint’ to reveal the answer.
| Multiply one by ten |
Now, let’s consider the number ten.
What do you need to do to the number ten so that it can be in the hundreds place instead of the tens place?
Press ‘Hint’ to reveal the answer.
| Multiply ten by ten |
In the base-10 place value system, what mathematical operation is used every time to move from the ones place to the tens place; tens to hundreds; hundreds to thousands; thousands to ten thousands; ten thousands to hundred thousands?
Press ‘Hint’ to reveal the answer.
| Multiplying by ten |

Multiplying by 10
Each time you move a number one place value to the left, it is the same as multiplying that number by ten. The number gets bigger by a factor of ten.
| Tens place | |
| Hundreds place | |
| One thousands place | |
| Ten thousands place | |
| Hundred thousands place |
Explore the following place value chart.

A place value chart representing six place values. The chart starts at the ones place value on the right side, and ends at the hundred thousands place value on the left side. When you multiply the ones place by ten, you move one place value left to the tens place. When you multiply the tens place by ten, you move one place value left to the hundreds place. When you multiply the hundreds place by ten, you move one place value left to the thousands place. When you multiply the thousands place by ten, you move one place value left to the ten thousands place. When you multiply the ten thousands place by ten, you move one place value left to the hundred thousands place. The ones, tens, and hundreds places are the first grouping of three place values to the left of a decimal point. The thousands, ten thousands, and hundred thousands places are the second grouping of three place values to the left of a decimal point.
Dividing by 10
Similarly, each time you move a number one place value to the right, it is the same as dividing that number by ten. The number gets smaller by a factor of ten.
- What mathematical operation is used to move from the hundred thousands place to the hundreds place?
Record your response using a method of your choice.
Press ‘Hint’ to reveal the solution and a place value chart.
| Dividing by one thousand | |
| Move three place values to the right |
|

A place value chart representing six place values. The chart starts at the ones place value on the right side, and ends at the hundred thousands place value on the left side. When you divide the hundred thousands place by ten, you move one place value right to the ten thousands place. When you divide the ten thousands place by ten, you move one place value right to the thousands place. When you divide the thousands place by ten, you move one place value right to the hundreds place. When you divide the hundreds place by ten, you move one place value right to the tens place. When you divide the tens place by ten, you move one place value right to the ones place. The ones, tens, and hundreds places are the first grouping of three place values to the left of a decimal point. The thousands, ten thousands, and hundred thousands places are the second grouping of three place values to the left of a decimal point.
Action
Converting measurements between metric units
Explore the following representation of base-10 relationships in the metric system.

Seven steps representing the base-ten relationships between metric units. The steps start in the top-left corner and end in the bottom-right corner. The centre step represents the ones place and is labelled “unit.” For example: one metre, one gram, or one litre. To convert a measurement up to the next largest metric unit, we divide by ten. The first step up and to the left of the ones place represents the tens place and is labelled “deca,” a prefix that means ten. One unit equals zero-point-one deca-units. The next step up and to the left represents the hundreds place and is labelled “hecto,” a prefix that means one hundred. One unit equals zero-point-zero-one hecto-units. The next step up and to the left represents the thousands place and is labelled “kilo,” a prefix that means one thousand. One unit equals zero-point-zero-zero-one kilo-units. To convert a measurement down to the next smallest metric unit, we multiply by ten. The first step down and to the right of the ones place represents the one tenths place and is labelled “deci,” a prefix that means one tenth or zero-point-one. One unit equals ten deci-units. The next step down and to the right represents the one hundredths place and is labelled “centi,” a prefix that means one hundredth or zero-point-zero-one. One unit equals one hundred centi-units. The next step down and to the right represents the one thousandth place and is labelled “milli,” a prefix that means one thousandth or zero-point-zero-zero-one. One unit equals one thousand milli-units.
Let’s practice converting measurements to different metric units. If you need help, review the representation of base-10 relationships in the metric system. For each metric unit conversion, select the corresponding number that would result from the conversion.
Powers of 10
We know how to calculate the expression
This expression can also be written using exponents as (or the number ten multiplied by itself two times).

Ten to the power of two (or ten squared) is an exponential expression representing the number ten being multiplied by itself two times. The number ten is called the base and the number two is called the exponent, while the entire expression is called the power.
We can use the letter to represent the exponent in exponential expressions, where equals the number of times to multiply or divide the base:
Powers of 10 with a positive exponent
A positive exponent indicates how many times to multiply a base number.
When the exponent is positive on a power of ten (n > 0), we move the number 1 n-amount of place values to the left of the decimal point. There will be n-amount of zeros after the number 1.
Explore the following example of a power of ten with a positive exponent.
| Ten to the power of six | ||
|---|---|---|
| Exponential form | Factored form | Standard form |
| 106 | 10 × 10 × 10 × 10 × 10 × 10 | 1,000,000 |
Powers of 10 with a negative exponent
A negative exponent indicates how many times to divide a base number.
When the exponent is negative on a power of ten (n < 0), we move the number 1 n-amount of place values to the right of the decimal point. There will be n-amount of zeros before the number 1.
Explore the following example of a power of ten with a negative exponent.
| Ten to the power of negative two | ||
|---|---|---|
| Exponential form | Factored form | Standard form |
|
or |
or |
0.01
or |
- What do you think ten to the power of zero will be?
Record your answer using a method of your choice.
Calculating powers of 10
Let's practice calculating powers of ten with positive and negative exponents.
Complete the Calculating Powers of 10 Table in your notebook or using the following fillable and printable document.
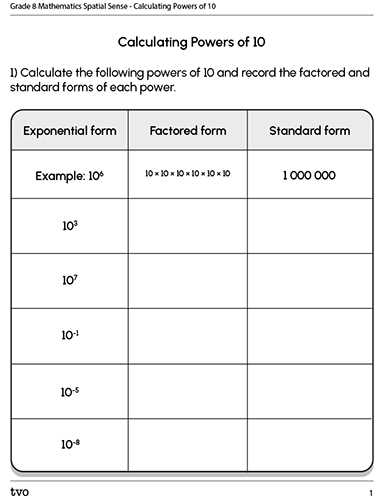
Press the Activity button to access the Calculating Powers of 10 Table.
Activity (Open PDF in a new tab)Press ‘Suggested Answer’ to reveal possible solutions.
| Solution to question one | ||
| Exponential form | Factored form | Standard form |
| 10 × 10 × 10 | 1,000 | |
| 10 × 10 × 10 × 10 × 10 × 10 × 10 | 10,000,000 | |
|
1 ÷ 10 or |
0.1
or |
|
|
1 ÷ (10 × 10 × 10 × 10 × 10) or |
0.00001
or |
|
|
1 ÷ (10 × 10 × 10 × 10 × 10 × 10 × 10 × 10) or |
0.00000001
or |
|
| Solution to question two |
| When the exponent is positive in a power of 10, you move the number 1 to the left on a place value chart. |
| Solution to question three |
| When the exponent is negative in a power of 10, you move the number 1 to the right on a place value chart. |
Very large and very small numbers
There are many different metric prefixes that can be used to name very large and very small numbers.
Explore the following number line representing very large and very small metric measurements, and the approximate size of different objects.

A number line representing very large metric units. The number line includes the metric prefixes and the approximate size of different objects.
On the Very Large Metric Units number line, the mark on the right represents the base unit and is labelled “metre.” One metre is equal to metres. The metric measurements and object size get larger as you move left from the base unit. The first mark to the left of the base unit is labelled “kilo.” One kilometre is equal to metres. The second mark to the left of the base unit is labelled “mega.” One megametre is equal to metres. The third mark to the left of the base unit is labelled “giga.” One gigametre is equal to metres. The fourth mark to the left of the base unit is labelled “tera.” One terametre is equal to metres. The fifth mark to the left of the base unit is labelled “peta.” One petametre is equal to metres. The sixth mark to the left of the base unit is labelled “exa.” One exametre is equal to metres. The seventh mark to the left of the base unit is labelled “zetta.” One zettametre is equal to metres. The eighth mark to the left of the base unit is labelled “yotta.” One yottametre is equal to metres. The ninth mark to the left of the base unit is labelled .
The Very Large Metric Units number line lists the approximate size of the following objects. The size of the observable universe is approximately metres. The size of the Milky Way galaxy is approximately metres. The size of one parsec is approximately metres. The size of one lightyear is approximately metres. The distance from the Earth to the Sun is approximately metres. The size of the Sun is approximately metres. The size of the Earth is approximately metres. The size of a city is approximately metres. The size of a mountain is approximately metres. The size of a house is approximately metres. The size of a person is approximately metres.

A number line representing very small metric units. The number line includes the metric prefixes and the approximate size of different objects.
On the Very Small Metric Units number line, the mark on the left represents the base unit and is labelled “metre.” One metre is equal to metres. The metric measurements and object size get smaller as you move right from the base unit. The first mark to the right of the base unit is labelled “milli.” One millimetre is equal to metres. The second mark to the right of the base unit is labelled “micro.” One micrometre is equal to metres. The third mark to the right of the base unit is labelled “nano.” One nanometre is equal to metres. The fourth mark to the right of the base unit is labelled “pico.” One picometre is equal to metres. The fifth mark to the right of the base unit is labelled “femto.” One femtometre is equal to metres. The sixth mark to the right of the base unit is labelled “atto.” One attometre is equal to metres. The seventh mark to the right of the base unit is labelled “zepto.” One zeptometre is equal to metres. The eighth mark to the left of the base unit is labelled “yotto.” One yottometre is equal to metres.
The Very Small Metric Units number line lists the approximate size of the following objects. The size of a finger is approximately metres. The size of a hair Is approximately metres. The size of a microbe is approximately metres. The size of a cell is approximately metres. The size of DNA is approximately metres. The size of a molecule is approximately metres. The size of an atom is approximately metres. The size of a nucleus is approximately metres. The size of a proton is approximately metres. The size of a quark is approximately metres.

The Milky Way Galaxy
Cells under a microscope
The unit of measurement on the number line is metres. To name a metric measurement we just add the unit after the appropriate prefix, for example: “micrometre” or “terametre.”
- How many of the metric prefixes have you heard of before?
- Which metric prefixes are new to you?
Record your answers using a method of your choice.
Determining standard form using powers and prefixes
Let’s practice determining the standard form of numbers based on their powers and metric prefixes.
For each sentence, select the missing number from the drop-down menu.
Consolidation
Metric prefixes
Explore the following metric prefix scale.

A number line representing metric prefixes and their symbols. The centre mark represents is labelled "unit," for example: one metre, one gram, or one litre. One unit is equal to . The metric measurements get larger as you move left from the centre (or unit). The first mark to the left of the unit is labelled "deca." One deca-unit is equal to , and its symbol is the lower-case letters "da." The second mark to the left of the unit is labelled "hecto." One hecto-unit is equal to , and its symbol is the lower-case letter "h." The third mark to the left of the unit is labelled "kilo." One kilo-unit is equal to , and its symbol is the lower-case letter "k." The fourth mark to the left of the unit is labelled "mega." One mega-unit is equal to , and its symbol is the upper-case letter "M." The fifth mark to the left of the unit is labelled "giga." One giga-unit is equal to , and its symbol is the upper-case letter "G." The sixth mark to the left of the unit is labelled "tera." One tera-unit is equal to , and its symbol is the upper-case letter "T." The metric measurements get smaller as you move right from the centre (or unit). The first mark to the right of the unit is labelled "deci." One deci-unit is equal to , and its symbol is the lower-case letter "d." The second mark to the right of the unit is labelled "centi." One centi-unit is equal to , and its symbol is the lower-case letter "c." The third mark to the right of the unit is labelled "milli." One milli-unit is equal to , and its symbol is the lower-case letter "m." The fourth mark to the right of the unit is labelled "micro." One micro-unit is equal to , and its symbol is the Greek letter "mu." The fifth mark to the right of the unit is labelled "nano." One nano-unit is equal to , and its symbol is the lower-case letter "n." The sixth mark to the right of the unit is labelled "pico." One pico-unit is equal to , and its symbol is the lower-case letter "p."
When we convert a measurement to a larger metric unit, we move the decimal point to the left (or divide).
When we convert a measurement to a smaller metric unit, we move the decimal point to the right (or multiply).
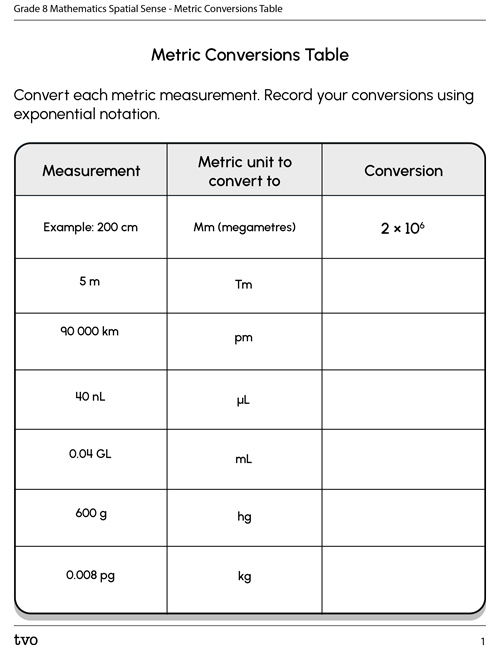
Use the metric prefix scale to complete the Metric Conversions Table in your notebook or using the following fillable and printable document. You can also record your metric conversions using a method of your choice.
Press ‘Suggested Answer’ to reveal the solutions.
| Measurement | Metric unit to convert to | Conversion (in exponential notation) |
| 5 m | Tm (terametres) | |
| 90,000 km | pm (picometres) | |
| 40 nL | µL (microlitres) | |
| 0.04 GL | mL (millilitres) | |
| 600 g | hg (hectogram) | |
| 0.008 pg | kg (kilogram) |
- What are the benefits to understanding and using metric conversions?
- Provide 3 examples of when converting metric measurements would be helpful to you in everyday life.
Record your responses using a method of your choice.
Reflection
As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.
I feel...
Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.
When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.
Discover MoreZero and the Place Value System are foundational concepts in mathematics.
- Which cultures created and developed these systems?
Record your response using a method of your choice, then create a representation of mathematical contributions from different cultures.
Connect with a TVO Mathify tutor
Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.
TVO Mathify (Opens in a new window)