Minds On

Recognizing angles

We know that angles can measure from 0° to 360° (or a full rotation).

Brainstorm

Types of angles

What different types of angles can you think of?

Record your response using a method of your choice.

Use your brainstorm and knowledge of angles to match the following images and descriptions of angles.

For each image of an angle, select the corresponding name and description.

Action

Supplementary, complementary, and opposite angles

We reviewed the names of single angles in our Minds On activity.

Let’s explore the names for pairs of angles.

Press each ‘Angle’ tab to explore a description of an angle pair.

Two angles that have a sum of 90° are called complementary angles. A 30-degree angle and a 60-degree angle are complementary angles because their sum equals 90 degrees.

Two angles that have a sum of 180° are called supplementary angles. A 120-degree angle and a 60-degree angle are supplementary angles because their sum equals 180-degrees.

When two lines intersect, they form two pairs of opposite angles. Opposite angles always measure the same number of degrees.

The sum of the two pairs of opposite angles always equals 360° because the sum of the four angles resulting from two intersecting lines displays a full rotation.

Two straight lines intersect forming angles A, B, C, and D. Angle A and angle C are opposite angles and both measure 120 degrees. Angle B and angle D are opposite angles and both measure 60 degrees.

Calculating missing angle measurements

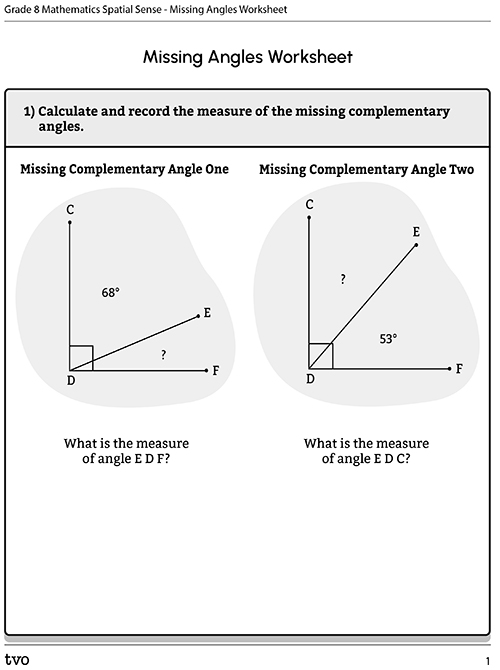
Complete the Missing Angles Worksheet in your notebook or using the following fillable and printable documents. You can also record your answers using a method of your choice.

Press the Activity button to access the Missing Angles Worksheet.

Activity (Open PDF in a new tab)

Press ‘Suggested Answers’ to reveal the solutions.

Solution to question one:
The sum of two complimentary angles always equals 90°.
90 ° - ∠ E D C = ∠ E D F 90 - 68 = 22 ∠ E D F = 22 °
90 ° - ∠ E D F = ∠ E D C 90 - 53 = 37 ∠ E D C = 37 °
Solution to question two:
The sum of two supplementary angles always equals 180°.
180 ° - ∠ B A D = ∠ B A C 180 - 94 = 86 ∠ B A C = 86 °
180 ° - ∠ B A C = ∠ B A D 180 - 43 = 137 ∠ B A D = 137 °
Solution to question three:
Opposite angles always measure same number of degrees.
∠ R Q S = ∠ T Q P

∠ T Q S = ∠ R Q P

∠ R Q S = 16 °

∠ T Q S = 74 °

∠ T Q P = ∠ R Q S

∠ T Q S = ∠ R Q P

∠ T Q P = 83 °

∠ T Q S = 97 °

Transversals

A transversal is any line that crosses another line or multiple lines.

In geometry, we usually work with transversals when they cross parallel lines, like the two tracks of a railroad.

Two parallel lines at an angle from the top right to the bottom left. A third line vertically intersects the set of parallel lines and is called a transversal.

Let’s practice creating a transversal.

Press the ‘TVO Mathify’ button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.

You can also record a detailed description of your transversal using a method of your choice.

TVO Mathify (Opens in a new window) Activity(Open PDF in a new window)

Press ‘Suggested Answer’ to reveal a possible solution.

Parallel lines B E and A R are positioned horizontally. Line O W intersects lines B E and A R at an angle from the top right to the bottom left. Line O W is a transversal.

Transversal angles

Transversal OW from our previous activity creates eight angles where it crosses lines BE and AR.

Parallel lines B E and line A R are positioned horizontally. Line O W intersects lines B E and A R at an angle from the top right to the bottom left. Line O W is a transversal. The intersection of line O W and line B E creates the angles O Q B, O S E, W T B, and W U E. The intersection of line O W and A R creates the angles O V A, O X R, W Y A, and W Z R.

Notice that the pairs of angles along each straight line are supplementary angles, or angles whose sum equals 180°.

Transversals also create other pairs of angles that follow different patterns we can use to determine the size of unknown angles.

Transversal angle patterns

When the two lines crossed by a transversal are parallel lines, angle patterns are created.

Let’s explore the names for transversal angle pairs and the patterns they create.

Press each ‘Angle’ tab to explore the various transversal angle patterns.

The angles that are located on the either side of a transversal and on the interior (or inside) of parallel lines are called interior angles.

Co-interior angles are the pairs of interior angles that are located on the same side of a transversal and on different parallel lines. Co-interior angles are supplementary because they always have a sum of 180°.

Explore the following example of co-interior angles.

Parallel lines B E and line A R are positioned horizontally. Line O W intersects lines B E and A R at an angle from the top right to the bottom left. Line O W is a transversal. The intersection of line O W with lines B E and A R creates the interior angles O V A, O X R, W T B, and W U E.

  • ∠ O V A and ∠ W T B are co-interior angles and have a sum of 180°.
  • ∠ O X R and ∠ W U E are co-interior angles and have a sum of 180°.

Notice that the co-interior angles create a ‘C’-shaped pattern with the transversal and two parallel lines. This ‘C’ shape can face any direction depending on the orientation of the intersecting lines.

The angles that are located on different sides of a transversal and on different parallel lines are called alternate angles. Alternate angles are congruent because they always have equal measures.

Alternate interior angles are the pairs of alternate angles located on different sides of a transversal and on the interior (or inside) of different parallel lines.

Explore the following example of alternate interior angles.

Line B E and line A R travel in parallel horizontally. Line O W travels through lines B E and A R at an angle from the top right to the bottom left. Line O W is a transversal. The intersection of line O W with lines B E and A R creates the interior angles O V A, O X R, W T B, and W U E.

  • ∠ O V A and ∠ W U E are alternate interior angles and have equal measures.
  • ∠ O X R and ∠ W T B are alternate interior angles and have equal measures.

Alternate exterior angles are the pairs of alternate angles located on different sides of a transversal and on the exterior (or outside) of different parallel lines.

Explore the following example of alternate exterior angles.

Parallel lines B E and line A R are positioned horizontally. Line O W intersects lines B E and A R at an angle from the top right to the bottom left. Line O W is a transversal. The intersection of line O W with lines B E and A R creates the exterior angles O Q B, O S E, W Y A, and W Z R.

  • ∠ O Q B and ∠ W Z R are alternate exterior angles and have equal measures.
  • ∠ O S E and ∠ W Y A are alternate exterior angles and have equal measures.

Notice that both the alternate interior and alternate exterior angles create a ‘Z’-shaped pattern with the transversal and two parallel lines. This ‘Z’ shape can face any direction depending on the orientation of the intersecting lines.

Corresponding angles are the pairs of interior and exterior angles that are located on the same side of a transversal and on different parallel lines. Corresponding angles are congruent because they always have equal measures.

Explore the following example of corresponding angles.

Parallel lines B E and line A R are positioned horizontally. Line O W intersects lines B E and A R at an angle from the top right to the bottom left. Line O W is a transversal. The intersection of line O W with lines B E and A R creates the interior angles O V A, O X R, W T B, and W U E, and the exterior angles O Q B, O S E, W Y A, and W Z R.

  • ∠ O Q B and ∠ O V A are corresponding angles and have equal measures.
  • ∠ W T B and ∠ W Y A are corresponding angles and have equal measures.
  • ∠ O S E and ∠ O X R are corresponding angles and have equal measures.
  • ∠ W U E and ∠ W Z R are corresponding angles and have equal measures.

Notice that corresponding angles create an ‘F’-shaped pattern with the transversal and two parallel lines. This ‘F’ shape can face any direction depending on the orientation of the intersecting lines.

Determining missing angles using transversal angle patterns

Complete the Transversal Angles Worksheet in your notebook or using the following fillable and printable documents. You can also record your answers using a method of your choice.

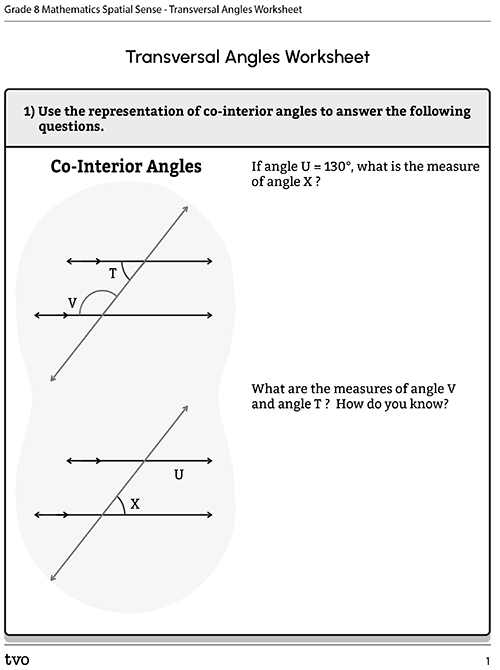
Press the Activity button to access the Transversal Angles Worksheet.

Activity (Open PDF in a new tab)

Press ‘Suggested Answers’ to reveal the solutions.

Solution to question one:

The sum of co-interior angles always equals 180°.

180° - ∠ U = ∠ X

180 - 130 = 50

∠ X = 50°

∠ T and ∠ U are supplementary angles. ∠ V and ∠ X are supplementary angles.

The sum of supplementary angles always equals 180°.

180° - ∠ U = ∠ T

180° - ∠ X = ∠ V

180 - 130 = 50

180 - 50 = 130

∠ T = 50°

∠ V = 130°

Solution to question two:

Alternate interior angles are located on the inside of different parallel lines and form a Z-shaped pattern.

∠ T and ∠ X are alternate interior angles. ∠ U and ∠ V are alternate interior angles.

Alternate exterior angles are located on the outside of different parallel lines and form a Z-shaped pattern.

∠ Q and ∠ Z are alternate exterior angles. ∠ S and ∠ Y are alternate exterior angles.

Alternate angles always have equal measures.

∠ X = ∠ T

∠ X = 88°

∠ Z = ∠ Q

∠ Z = 130°

Solution to question three:

Corresponding angles are a pair of interior and exterior angles located on the same side of a transversal and on different parallel lines, and form an F-shaped pattern.

Corresponding angles always have equal measures.

∠ Y = ∠ T

∠ Y = 88°

∠ V = ∠ Q

∠ V = 130°

Consolidation

Describing angle relationships

Let’s use our knowledge of transversal angles to describe the relationships between known and unknown angles.

Complete the Angle Relationships Worksheet in your notebook or using the following fillable and printable documents.

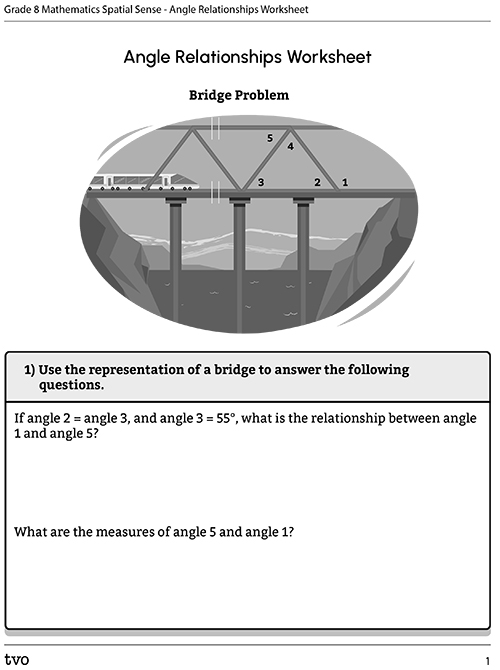
Press the Activity button to access the Angle Relationships Worksheet.

Activity (Open PDF in a new tab)

Press ‘Suggested Answers’ to reveal the the solutions.

Solution to question one:
∠ 1 and ∠ 2 are supplementary angles. ∠ 2 and ∠ 3 are congruent. ∠ 3 and ∠ 5 are alternate interior angles.
Alternate angles always have equal measures
∠ 5 = ∠ 3 ∠ 5 = 55°
The sum of two supplementary angles always equals 180°.
180 ° - ∠ 2 = ∠ 1 180 - 55 = 125 ∠ 1 = 125°
Solution to question two:
∠ 1 = ∠ 5 ∠ 2 = ∠ 6 ∠ 3 = ∠ 7 ∠ 4 = ∠ 8
Each pair of angles have equal measures because they are corresponding angles.
∠ 3 = ∠ 5 ∠ 4 = ∠ 6
Each pair of angles have equal measures because they are alternate angles.
∠ 3 + ∠ 6 = 180° ∠ 4 + ∠ 5 = 180°
The sum of each pair of angles equals 180° because they are co-interior angles.

Think about your learning

  1. What have you learned about parallel lines and angle relationships?
  2. What do you think is the most important information for others to understand?

Record your responses using a method of your choice.

Reflection

As you read the following descriptions, select the one that best describes your current understanding of the learning in this activity. Press the corresponding button once you have made your choice.

I feel...

Now, expand on your ideas by recording your thoughts using a voice recorder, speech-to-text, or writing tool.

When you review your notes on this learning activity later, reflect on whether you would select a different description based on your further review of the material in this learning activity.

Connect with a TVO Mathify tutor

Think of TVO Mathify as your own personalized math coach, here to support your learning at home. Press ‘TVO Mathify’ to connect with an Ontario Certified Teacher math tutor of your choice. You will need a TVO Mathify login to access this resource.

TVO Mathify (Opens in a new window)