Minds On

Parts of a circle

For each term, select the corresponding definition.

Press 'Let's check!' to reveal parts of a circle.

Description

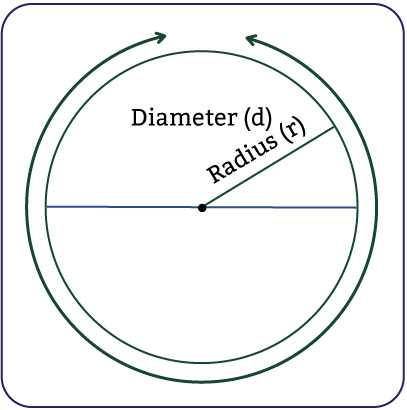
This is a diagram illustrating the circumference, diameter, and radius of a circle.

The circumference is represented by the capital letter “C.” The circumference is the distance around the outside edge of a circle. This is an identical concept to calculating the perimeter of a polygon. On the diagram, the circumference is the arrow that goes around the entire circle.

The diameter is represented by the lowercase letter “d.” The diameter is the distance across the circle, that goes through the centre of the circle. On the diagram, the diameter is the arrow that goes from one end of the circle to the other.

The radius is represented by the lowercase letter “r.” The radius is the distance halfway across the circle, which is equal to half of the diameter’s length. To calculate the radius, you can divide the diameter by 2. On the diagram, the radius is the arrow that starts from the centre of the circle and crosses to a point in the circle.

Explore

Let's explore this video entitled "Area of a Circle Formula" to learn more about the area of a circle.

Action

Understanding circumference of a circle

The circumference of a circle is the distance around the outside edge of a circle.

This concept is identical to the concept of calculating the perimeter of a polygon.

However, since a circle has no sides, we need to think a little differently about how to calculate its circumference.

One strategy which can be used to find the circumference is by using string to explore the circumference of the shape. To find the circumference, we can wrap a string around the circle.

Measuring

A piece of string is an example of something that can be used to help measure length.

Let's explore the following steps to measure the circumference of a circular object:

Step 1

To begin, we can use a length of string or another method of measurement to wrap around a circular object. This might be a bowl, a trash can, a coffee cup, a basketball hoop, or any circular object around you.

Student measuring circumference of bowl with a coloured string around the rim.

After measuring the object, take that piece of string and cut it or mark the measurement. Note that you are now working with a piece of string that is equal to the circumference of your object.

Step 2

Next, use the same piece of string to measure the diameter of the circular object. Start from one spot on the edge of the circle to a spot on the opposite side (trying to go through the centre). Now, cut or mark that piece.

Student measuring the diameter of a bowl with a string from one end to another.

Let's use what's left of your string to measure the diameter again. Cut or mark that measurement. Continue to do this until the string is too short to measure the diameter.

Step 3

In the end, the piece of string that was the measure of the circumference should be cut into 3 equal pieces, and a shorter piece. That little piece of string that was left over, should be just over one tenth of the other pieces.

Student measuring 4 pieces of string with a ruler.

These steps can be compared to actual calculations.

Take the circumference of a circle and divide it by the diameter, you will always end up with 3.14 or π.

No matter the circle, the value of the circumference to diameter will be approximately 3.14.

This can also be represented as:

Circumference ÷ Diameter = approximately 3.14

3.14 is the value of pi or π.

So, if Circumference ÷ Diameter = approximately 3.14, we can deduce a formula for the circumference as:

Circumference = π × Diameter

Circumference = πd

Student Tips

Did you know?

Recall that the diameter is double the radius for any circle.

So, we can write d = 2 × r or d = 2r

Circumference = πd, which is the same as Circumference = π × 2r

Circumference of a circle = 2πr

Calculating the circumference

Now that you understand the relationship between circumference and diameter and have explored the formula for calculating the circumference of a circle, let's apply the formula!

If you would like, you can complete the next series of calculations using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.

Press the ‘TVO Mathify' button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.

Activity

Press 'Let's check!' to reveal the calculations for the activity Calculating the Circumference.

Let's check!

Check out the calculations for the Calculating the Circumference activity:

1. With $\begin{aligned} d & = 5 m, \\ C & = π \times 5 m \\ C & = 15.7 m \end{aligned}$

2. With $\begin{aligned} r & = 6.3 m, \\ C & = 2 π (6.3 m) \\ C & = 39.6 m \end{aligned}$

3. With $\begin{aligned} C & = 5.8 c m, \\ C & = π d \\ 5.8 c m & = π d \\ d & = 5.8 c m \div π \\ d & = 1.8 c m \end{aligned}$

4. With $\begin{aligned} C & = 14.2 c m, \\ C & = π d \\ 14.2 c m & = π d \\ d & = 14.2 \div π \\ d & = 4.5 c m \end{aligned}$

To find the radius, we can divide the diameter by 2:

$\begin{aligned} r & = 4.5 c m \div 2 \\ r & = 2.25 c m \end{aligned}$

Area of a circle

Student Tips

The formula

To calculate the area of a circle, we use the following formula:

$A = π r^{2}$

"A" represents the area
"r" represents the radius
$π = 3.14 \dots$

Part 1: Exploring the formula

If you would like, you can complete the next series of word problems using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.

Press the ‘TVO Mathify' button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.

Activity

Press 'Let's check!' to reveal the calculations for the activity Exploring the Area of a Circle.

Let's check!

Question 1	$A = π r^{2}$ $A = π {(7)}^{2}$ $A = 153.9 {cm}^{2}$ The amount of cardboard the restaurant will need is 153.9 cm²
Question 2	$A = π r^{2}$ $A = π {(6)}^{2}$ $A = 113.1 m^{2}$ The amount of pool cover material we will need is 113.1 m²

Question 1

$A = π r^{2}$

$A = π {(7)}^{2}$

$A = 153.9 {cm}^{2}$

The amount of cardboard the restaurant will need is 153.9 cm²

Question 2

$A = π r^{2}$

$A = π {(6)}^{2}$

$A = 113.1 m^{2}$

The amount of pool cover material we will need is 113.1 m²

Part 2: Calculate using the formula

Now that we have explored how the formula for the area of a circle is derived, let's apply it to word problems.

If you would like, you can complete the next series of word problems using TVO Mathify or a method of your choice. You can also use your notebook or the following fillable and printable document.

Press the ‘TVO Mathify' button to access this interactive whiteboard and the ‘Activity’ button for your note-taking document. You will need a TVO Mathify login to access this resource.

Activity

Press 'Let's check!' to reveal the calculations for the activity Calculating the Area of a Circle.

Let's check!

Question 1	$A = π r^{2}$ $A = π (10)^{2}$ $A = 314 m^{2}$ The area of the circle is 314 m²
Question 2	$A = π r^{2}$ $A = π (5.2)^{2}$ $A = 84.95 {km}^{2}$ The area of the circle is 84.95 km²

Question 1

$A = π r^{2}$

$A = π (10)^{2}$

$A = 314 m^{2}$

The area of the circle is 314 m²

Question 2

$A = π r^{2}$

$A = π (5.2)^{2}$

$A = 84.95 {km}^{2}$

The area of the circle is 84.95 km²